题目内容
【题目】(1)因式分解:-28m3n2+42m2n3-14m2n
(2)因式分解:9a2(x-y)+4b2(y-x)
(3)求不等式![]() 的负整数解
的负整数解
(4)解不等式组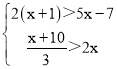 ,把它们的解集在数轴上表示出来.
,把它们的解集在数轴上表示出来.
【答案】(1)-14m2n(2mn-n2+1);(2)(x-y)(3a+2b)(3a-2b);(3)负整数解有-3,-2,-1;(4)x<2,见解析
【解析】
(1)直接提取公因式因式分解求解即可;
(2)此多项式有公因式,应先提取公因式,再对余下的多项式进行观察,有2项,可采用平方差公式继续分解.
(3)先去分母,再去括号,移项,合并同类项,把x的系数化为1,再求出它的负整数解即可;
(4)分别求出各不等式的解集,再求出其公共解集,把它们的解集在数轴上表示出来即可.
解:(1)-28m3n2+42m2n3-14m2n=-14m2n(2mn-n2+1);
(2)9a2(x-y)+4b2(y-x)
=(x-y)(9a2-4b2)
=(x-y)(3a+2b)(3a-2b);
(3)![]() ,
,
2x≤6+3(x-1),
2x≤6+3x-3,
2x-3x≤6-3,
-x≤3,
x≥-3,
故负整数解有-3,-2,-1.
(4)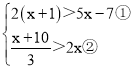 ,
,
解不等式①得:x<3,
解不等式②得:x<2,
故原不等式组的解集为:x<2,
在数轴上表示出来为:
![]()

 阅读快车系列答案
阅读快车系列答案【题目】某自行车厂计划一周生产1400辆自行车,平均每天生产200辆,由于各种原因,实际每天的生产量与计划量相比有出入。
下表是某周的生产情况(超产为正,减产为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 |
|
|
|
|
|
|
|
(1)根据记录可知前三天共生产了_________辆;
(2)产量最多的一天比产量最少的一天多生产__________辆;
(3)该厂实行计件工资制,每辆车60元,超额完成任务每辆奖15元,少生产一辆扣15元,那么该厂工人这一周的工资总额是多少?