题目内容
【题目】长江汛期即将来临,防汛指挥部在一危险地带两岸各安置了一探照灯,便于夜间查看江水及两岸河堤的情况.如图1,灯A射线自AM顺时针旋转至AN便立即回转,灯B射线自BP顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是a°/秒,灯B转动的速度是b°/秒,且a、b满足|a-3b|+(a+b-4)=0.假定这一带长江两岸河堤是平行的,即PQ∥MN,且∠BAN=45°
(1)求a、b的值;
(2)若灯B射线先转动20秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?
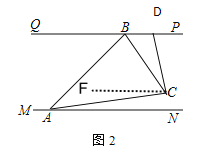
(3)如图2,两灯同时转动,在灯A射线到达AN之前.若射出的光束交于点C,过C作CD⊥AC交PQ于点D,则在转动过程中,∠BAC与∠BCD的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请求出其取值范围.

【答案】(1)a=3,b=1;(2)A灯转动10秒或85秒时,两灯的光束互相平行;(3)∠BAC与∠BCD的数量关系不发生变化,2∠BAC=3∠BCD.
【解析】
(1)根据非负数的性质列方程组求解即可;
(2)设A灯转动t秒,两灯的光束互相平行,分两种情况:①在灯A射线到达AN之前;②在灯A射线到达AN之后,分别列出方程求解即可;
(3)设A灯转动时间为t秒,则∠CAN=180°3t,∠BAC=∠BAN∠CAN=3t135°,过点C作CF∥PQ,则CF∥PQ∥MN,得出∠BCA=∠CBD+∠CAN=180°2t,∠BCD=∠ACD∠BCA=2t90°,即可得出结果.
解:(1)∵|a-3b|+(a+b-4)=0,
∴![]() ,
,
解得:![]() ,
,
故a=3,b=1;
(2)设A灯转动t秒,两灯的光束互相平行,
①在灯A射线到达AN之前,由题意得:3t=(20+t)×1,
解得:t=10,
②在灯A射线到达AN之后,由题意得:3t180°=180°(20+t)×1,
解得:t=85,
综上所述,A灯转动10秒或85秒时,两灯的光束互相平行;
(3)∠BAC与∠BCD的数量关系不发生变化,2∠BAC=3∠BCD;
理由:设A灯转动时间为t秒,则∠CAN=180°3t,
∴∠BAC=∠BAN∠CAN=45°(180°3t)=3t135°,
∵PQ∥MN,
如图2,过点C作CF∥PQ,则CF∥PQ∥MN,
∴∠BCF=∠CBD,∠ACF=∠CAN,
∴∠BCA=∠BCF+∠ACF=∠CBD+∠CAN=t+180°3t=180°2t,
∵CD⊥AC,
∴∠ACD=90°,
∴∠BCD=∠ACD∠BCA=90°(180°2t)=2t90°,
∴2∠BAC=3∠BCD.

【题目】“五一”期间,文具店老板购进100只两种型号的文具进行销售,其进价和售价之间的关系如下表:
型号 | 进价(元/只) | 售价(元/只) |
A型 | 10 | 14 |
B型 | 15 | 22 |
(1)老板如何进货,能使进货款恰好为1350元?
(2)要使销售文具所获利润不少于500元,那么老板最多能购进A型文具多少只?





