题目内容
【题目】如图，△ABC是边长为6 cm的等边三角形，动点P从A出发，以3 cm/s的速度，沿A-B-C向C运动，同时，动点Q从C出发沿CA方向以1 cm/s的速度向A运动，当其中一点运动到终点时，两点同时停止运动．设运动时间为t秒，当t= ____s，△APQ是直角三角形．
【答案】
或
【解析】
分析题意可知，需分两种情况讨论，①当∠QPA=90°时，②当∠PQA=90°时，分别作出图形，利用含30°角的直角三角形的性质列方程求解即可.
解：由题意可得，分两种情况讨论，
①当∠QPA=90°时，如图：
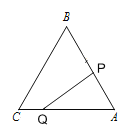
∵AC=6，CQ=t，AP=3t，
∴AQ=6-t，
∵∠A=60°，
∴AQ=2AP，即6-t=2×3t，
解得：t=；
②当∠PQA=90°时，如图：
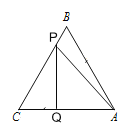
∵CQ=t，CP=12-3t，∠C=60°，
∴CP=2CQ，即12-3t=2t，
解得：t=，
综上所述，当t=或秒时，△APQ是直角三角形．
练习册系列答案
相关题目
【题目】某公司招聘外卖送餐员，送餐员的月工资由底薪1000元加上外卖送单补贴
送一次外卖称为一单
构成，外卖送单补贴的具体方案如下：
外卖送单数量 | 补贴 |
每月不超过500单 | 6 |
超过500单但不超过m单的部分 | 8 |
超过m单的部分 | 10 |
若某“外卖小哥”4月份送餐400单，则他这个月的工资总额为多少元？
设5月份某“外卖小哥”送餐x单
，所得工资为y元，求y与x的函数关系式．
若某“外卖小哥”5月份送餐800单，所得工资为6500元，求m的值．
