Question

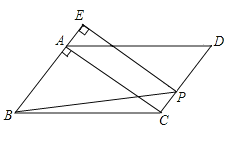
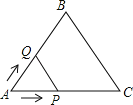
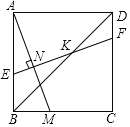
【题目】如图，在Rt△ABC中，∠B＝90°，BC＞AB，在BC边上取点D，使AB＝BD，构造正方形ABDE，DE交AC于点F，作EG⊥AC交AC于点G，交BC于点H．

（1）求证：EF＝DH；

（2）若AB＝6，DH＝2DF，求AC的长．

Answer 1

【答案】（1）见解析；（2）3

【解析】

（1）根据正方形的性质及同角的余角相等建立AAS即可证明△AFE≌△EHD，再根据全等三角形的性质即可得出答案；

（2）设DF＝x，则EF＝DH＝2x，根据AB＝6即可求出x的值；再证明△AEF∽△CDF即可求出BC的值，最后根据勾股定理即可得出答案．

解：（1）证明：在正方形ABDE中，AE＝ED，∠AEF＝∠EDH＝90°

∴∠DHE+∠GEF＝90°

∵EG⊥AC

∴∠GEF+∠GFE＝90°

∴∠GFE＝∠DHE

在△AFE和△EHD中

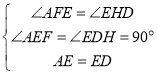
∴△AFE≌△EHD（AAS）

∴EF＝DH；

（2）∵DH＝2DF，EF＝DH

∴设DF＝x，则EF＝DH＝2x

∵AB＝6

∴AE＝DE＝6

∴x+2x＝6

∴x＝2

∴DF＝2，EF＝4

∵在正方形ABDE中，AE∥BD

∴△AEF∽△CDF

∴

∴

∴DC＝3

∴BC＝BD+DC＝6+3＝9

∴在Rt△ABC中，由勾股定理得：

AC＝＝＝

∴AC的长为．