题目内容
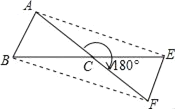
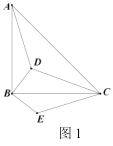
【题目】(1)已知如图1,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 内部,点
内部,点![]() 在
在![]() 外部,满足
外部,满足![]() ,且
,且![]() .求证:
.求证:![]() .
.
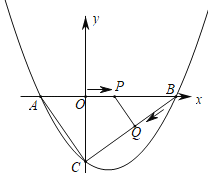
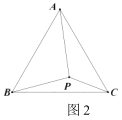
(2)已知如图2,在等边![]() 内有一点
内有一点![]() ,满足
,满足![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
【答案】(1)详见解析;(2)150°
【解析】
(1)先证∠ABD =∠CBE,根据SAS可证△ABD≌△CBE;
(2)把线段PC以点C为中心顺时针旋转60°到线段CQ处,连结AQ.根据旋转性质得△PCQ是等边三角形,根据等边三角形性质证△BCP≌△ACQ(SAS),得BP=AQ=4,∠BPC=∠AQC,根据勾股定理逆定理可得∠AQP=90°,进一步推出∠BPC=∠AQC=∠AQP+∠PQC=90°+60°.
(1)证明:∵∠ABC=90°,BD⊥BE
∴∠ABC=∠DBE=90°
即∠ABD+∠DBC=∠DBC+∠CBE
∴∠ABD =∠CBE.
又∵AB=CB,BD=BE
∴△ABD≌△CBE(SAS).
(2)如图,把线段PC以点C为中心顺时针旋转60°到线段CQ处,连结AQ.
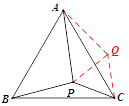
由旋转知识可得:
∠PCQ =60°,CP=CQ=3,
∴△PCQ是等边三角形,
∴CP=CQ=PQ=3.
又∵△ABC是等边三角形,
∴∠ACB=60°=∠PCQ,BC=AC,
∴∠BCP+∠PCA=∠PCA+∠ACQ,即∠BCP=∠ACQ.
在△BCP与△ACQ中
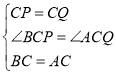
∴△BCP≌△ACQ (SAS)
∴BP=AQ=4,∠BPC=∠AQC.
又∵PA=5,
∴![]() .
.
∴∠AQP=90°
又∵△PCQ是等边三角形,∴∠PQC=60°
∴∠BPC=∠AQC=∠AQP+∠PQC=90°+60°=150°
∴∠BPC=150°.

练习册系列答案
相关题目