题目内容
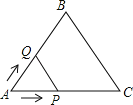
【题目】如图,等边△ABC的边长为2cm,点P从点A出发,以1cm/s的速度沿AC向点C运动,到达点C停止;同时点Q从点A出发,以2cm/s的速度沿AB﹣BC向点C运动,到达点C停止,设△APQ的面积为y(cm2),运动时间为x(s),则下列最能反映y与x之间函数关系的图象是( )
A.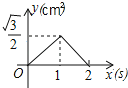 B.
B.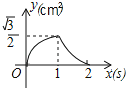
C.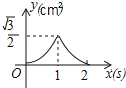 D.
D.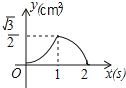
【答案】D
【解析】
根据点Q的位置分两种情况讨论,当点Q在AB上运动时,求得y与x之间函数解析式,当点Q在BC上运动时,求得y与x之间函数解析式,最后根据分段函数的图象进行判断即可.
解:由题得,点Q移动的路程为2x,点P移动的路程为x,
∠A=∠C=60°,AB=BC=2,
①如图,当点Q在AB上运动时,过点Q作QD⊥AC于D,则
AQ=2x,DQ=![]() x,AP=x,
x,AP=x,
∴△APQ的面积y=![]() ×x×
×x×![]() x=
x=![]() (0<x≤1),
(0<x≤1),
即当0<x≤1时,函数图象为开口向上的抛物线的一部分,故(A)、(B)排除;
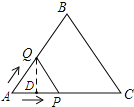
②如图,当点Q在BC上运动时,过点Q作QE⊥AC于E,则
CQ=4﹣2x,EQ=2![]() ﹣
﹣![]() x,AP=x,
x,AP=x,
∴△APQ的面积y=![]() ×x×(2
×x×(2![]() ﹣
﹣![]() x)=﹣
x)=﹣![]() +
+![]() x(1<x≤2),
x(1<x≤2),
即当1<x≤2时,函数图象为开口向下的抛物线的一部分,故(C)排除,而(D)正确;
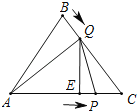
故选:D.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目