��Ŀ����
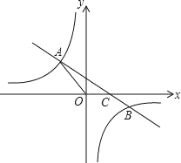
����Ŀ�����ǰ�һ����Բ�������ߵ�һ���ֺϳɵķ��ͼ�γ�Ϊ����Բ�������һ��ֱ���롰��Բ��ֻ��һ�����㣬��ô����ֱ�߽�������Բ�������ߣ���ͼ��ʾ����A��B��C��D�ֱ��ǡ���Բ����������Ľ��㣬��֪��D������Ϊ��0��-3����ABΪ��Բ��ֱ������ԲԲ��M������Ϊ��1��0������Բ�뾶Ϊ2��

��1�������������Բ�������߲��ֵĽ���ʽ����д���Ա�����ȡֵ��Χ��
��2���������������C�ġ���Բ�����ߵĽ���ʽ�����Կ���
��3�������Խ���һ�룬�����������������D�ġ���Բ�����ߵĽ���ʽ��
���𰸡���1��![]() ��
��![]() ����2��
����2��![]() ����3��
����3��![]() .
.
��������
��1����֪��![]() �������ʽΪ����ʽ��
�������ʽΪ����ʽ��![]() ������D���������⼴�ɣ�
������D���������⼴�ɣ�
��2���辭����C�ġ���Բ������CE��x���ڵ�E������CM����![]() �У��ɹ��ɶ�����֪OC������֪��C���꣬��ֱ�������οɵ�
�У��ɹ��ɶ�����֪OC������֪��C���꣬��ֱ�������οɵ�![]() ����
����![]() �У���ֱ�������οɵ�EM������֪��E���꣬��ֱ��CE�Ľ���ʽΪ
�У���ֱ�������οɵ�EM������֪��E���꣬��ֱ��CE�Ľ���ʽΪ![]() ������
������![]() ��
��![]() ��������⼴�ɣ�
��������⼴�ɣ�
��3�������![]() �ġ���Բ�����ߵĽ���ʽΪ
�ġ���Բ�����ߵĽ���ʽΪ![]() ���������֪����
���������֪����![]() ��������ȵ�ʵ����������
��������ȵ�ʵ����������![]() �ɵ�mֵ.
�ɵ�mֵ.
�⣺��1����ABΪ��Բ��ֱ������ԲԲ��M������Ϊ��1��0������Բ�뾶Ϊ2��֪![]() ��
��
�衰��Բ�������߲��ֵĽ���ʽΪ![]() ��
��
����![]() ����
����![]() ��
��![]() ��
��
���![]() ��
��
![]()
���ԡ���Բ�������߲��ֵĽ���ʽΪ![]() ���Ա�����ȡֵ��ΧΪ
���Ա�����ȡֵ��ΧΪ![]() ��
��
��2���辭����C�ġ���Բ������CE��x���ڵ�E������CM��

��![]() ��
�У�![]() �����ݹ��ɶ�����
�����ݹ��ɶ�����![]() ����
����![]() ��
��
![]()
![]()
��![]() ��
�У�![]()
![]()
![]()
![]()
��ֱ��CE�Ľ���ʽΪ![]() ��
��
����![]() ��
��![]() �����
�����
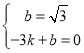
���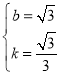
���Ծ�����C�ġ���Բ�����ߵĽ���ʽ![]() ��
��
��3�������![]() ������Բ�����ߵĽ���ʽΪ
������Բ�����ߵĽ���ʽΪ![]() ��
��
�������֪������![]() ֻ��һ��⣬
ֻ��һ��⣬
��![]() ��������ȵ�ʵ������
��������ȵ�ʵ������
�����![]()
![]()
���![]() ��
��![]() ����ȥ��
����ȥ��
���Ծ�����D������Բ�����ߵĽ���ʽΪ![]() .
.

 ��У����ϵ�д�
��У����ϵ�д�