题目内容
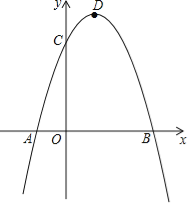
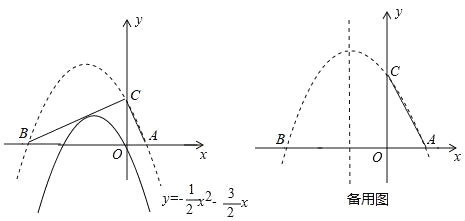
【题目】已知抛物线![]() 的图象如图所示:
的图象如图所示:
(1)将该抛物线向上平移2个单位,分别交x轴于A、B两点,交y轴于点C,则平移后的解析式为 .
(2)判断△ABC的形状,并说明理由.
(3)在抛物线对称轴上是否存在一点P,使得以A、C、P为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,说明理由.
【答案】(1)![]() ;(2)△ABC是直角三角形;(3)存在,
;(2)△ABC是直角三角形;(3)存在,![]() 、
、![]() 、
、![]() .
.
【解析】
(1)根据函数图象的平移规律,可得新的函数解析式;
(2)根据自变量与函数值的对应关系,可得A,B,C的坐标,根据勾股定理及逆定理,可得答案;
(3)根据等腰三角形的定义,分三种情况,可得关于n的方程,根据解方程,可得答案.
(1)将该抛物线向上平移2个单位,得:y![]() x2
x2![]() x+2.
x+2.
故答案为:y![]() x2
x2![]() x+2;
x+2;
(2)当y=0时,![]() x2
x2![]() x+2=0,解得:x1=﹣4,x2=1,即B(﹣4,0),A(1,0).
x+2=0,解得:x1=﹣4,x2=1,即B(﹣4,0),A(1,0).
当x=0时,y=2,即C(0,2).
AB=1﹣(﹣4)=5,AB2=25,AC2=(1﹣0)2+(0﹣2)2=5,BC2=(﹣4﹣0)2+(0﹣2)2=20.
∵AC2+BC2=AB2,∴△ABC是直角三角形;
(3)y![]() x2
x2![]() x+2的对称轴是x
x+2的对称轴是x![]() ,设P(
,设P(![]() ,n),AP2=(1
,n),AP2=(1![]() )2+n2
)2+n2![]() n2,CP2
n2,CP2![]() (2﹣n)2,AC2=12+22=5.分三种情况讨论:
(2﹣n)2,AC2=12+22=5.分三种情况讨论:
①当AP=AC时,AP2=AC2,![]() n2=5,方程无解;
n2=5,方程无解;
②当AP=CP时,AP2=CP2,![]() n2
n2![]() (2﹣n)2,解得:n=0,即P1(
(2﹣n)2,解得:n=0,即P1(![]() ,0);
,0);
③当AC=CP时,AC2=CP2,![]() (2﹣n)2=5,解得:n1=2
(2﹣n)2=5,解得:n1=2![]() ,n2=2
,n2=2![]() ,P2(
,P2(![]() ,2
,2![]() ),P3(
),P3(![]() ,2
,2![]() ).
).
综上所述:在抛物线对称轴上存在一点P,使得以A、C、P为顶点的三角形是等腰三角形,点P的坐标(![]() ,0),(
,0),(![]() ,2
,2![]() ),(
),(![]() ,2
,2![]() ).
).

 字词句段篇系列答案
字词句段篇系列答案【题目】(9分)九年级数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如下表:
售价(元/件) | 100 | 110 | 120 | 130 | … |
月销量(件) | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件60元,设售价为![]() 元.
元.
(1)请用含x的式子表示:①销售该运动服每件的利润是 元;②月销量是 件;(直接写出结果)
(2)设销售该运动服的月利润为![]() 元,那么售价为多少时,当月的利润最大,最大利润是多少?
元,那么售价为多少时,当月的利润最大,最大利润是多少?