题目内容
【题目】如图,在平行四边形ABCD中,AB=3,BC=5,对角线AC⊥AB.点P从点D出发,沿折线DC﹣CB以每秒1个单位长度的速度向终点B运动(不与点B、D重合),过点P作PE⊥AB,交射线BA于点E,连结BP.设点P的运动时间为t(秒),△BPE的面积为S(平方单位).
(1)AD与BC间的距离是 .
(2)当点P在BC上时,求PE的长(用含t的代数式表示).
(3)求S与t之间的函数关系式.
(4)直接写出PE将平行四边形ABCD的面积分成1:7两部分时t的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)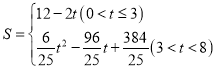 ;(4)t的值为
;(4)t的值为![]() 或
或![]()
【解析】
(1)过点A作AF⊥BC,垂足为F,在三角形ABC中依据勾股定理可求得AC的长,然后依据三角形的面积公式可求得AF的长,从而得到AD与BC之间的距离;
(2)由题意得出3<t<8,如图2所示;由题意可知PE∥AC,从而得到△BPE∽△BCA,由相似三角形的性质可知:![]() ,从而可求解;
,从而可求解;
(3)分0<t≤3时和3<t<8时两种情况,再根据相似三角形的性质进行解答即可;
(4)分0<t≤3时和3<t<8时两种情况,再根据PE将ABCD的面积分成1:7的两部分进行解答即可.
(1)过A作AF⊥BC于F点,如图1:

∵AC⊥AB,AB=3,BC=5,
∴AC=![]() ,
,
∴△ACB的面积=![]() AC×AB=
AC×AB=![]() BC×AF,
BC×AF,
解得:AF=![]() ,
,
∴AD与BC间的距离等于![]() .
.
故答案为:![]() ;
;
(2)∵AC⊥AB,
∴AC=![]() ,
,
当点P在BC上时,3<t<8,如图2:
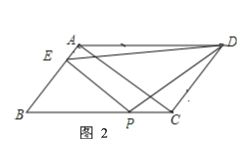
∵PE⊥AB,AC⊥AB,
∴PE∥AC,
∴△BPE∽△BCA,
∴![]() ,即
,即![]() ,
,
解得:PE=![]() ;
;
(3)∵边形ABCD是平行四边形,
∴AB∥CD,AB=CD=3,AD∥BC,AD=BC=5,
∵AC⊥AB,PE⊥AB,
∴AC∥PE,
①当0<t≤3时,
设PE与AD的交点为F,如图3:
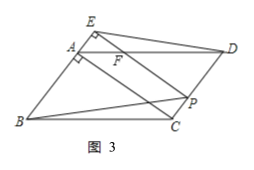
则四边形ACPE是平行四边形,
∴PE=AC=4,AE=PC=CD-PD=3-t,
∴BE=AB+AE=3+3-t=6-t,
∴S=![]() BE×PE=
BE×PE=![]() ×(6-t)×4=12-2t,
×(6-t)×4=12-2t,
即S与t之间的函数关系式为S=12-2t;
②当3<t<8时,如图4:
延长DC、EP交于点G,
则DG⊥EG,四边形AEGC是平行四边形,
∴GE=AC=4,AE=CG,
∵AB∥CD,
∴∠B=∠PCG,
∵∠BAC=∠PGC,
∴△CPG∽△BCA,
∴![]() ,即
,即![]() ,
,
解得:CG=![]() ,PG=
,PG=![]() ,
,
∴AE=CG=![]() ,PE=EG-PG=4-
,PE=EG-PG=4-![]() =
=![]() ,
,
∴BE=AB-AE=3-![]() =
=![]() ,
,
∴S=![]() BE×PE=
BE×PE=![]() ×
×![]()
![]() =
=![]() ,
,
即S与t之间的函数关系式为S=![]() ;
;
综上所述,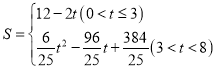
(4)PE将ABCD的面积分成1:7的两部分,ABCD的面积=AB×AC=3×4=12,
①当0<t≤3时,如图2所示:
∵AC⊥AB,PE⊥AB,
∴PF∥AC,
∴△DPF∽△DCA,
∴![]() ,即
,即![]() ,
,
解得:PF=![]() ,
,
∴△PDF的面积=![]() PD×PF=
PD×PF=![]() t2;
t2;
∴![]() ,
,
解得:t=![]() (负值舍去);
(负值舍去);
②当3<t<8时,如图4所示:
S=![]() ,
,
解得:t=![]() ,或t=
,或t=![]() (不符合题意,舍去).
(不符合题意,舍去).
综上所述,PE将平行四边形ABCD的面积分成1:7两部分时t的值为![]() 或
或![]() .
.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案