Question

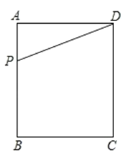
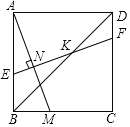
【题目】如图，已知正方形ABCD的边长为1，点M是BC边上的动点（不与B，C重合），点N是AM的中点，过点N作EF⊥AM，分别交AB，BD，CD于点E，K，F，设BM＝x．

（1）AE的长为______（用含x的代数式表示）；

（2）设EK＝2KF，则的值为______．

Answer 1

【答案】 x

【解析】

（1）根据勾股定理求得AM，进而得出AN，证得△AEN∽△AMB，由相似三角形的性质即可求得AE的长；

（2）连接AK、MG、CK，构建全等三角形和直角三角形，证明AK＝MK＝CK，再根据四边形的内角和定理得∠AKM＝90°，利用直角三角形斜边上的中线等于斜边的一半得NK＝AM＝AN，然后根据相似三角形的性质求得＝＝x，即可得出＝x．

（1）解：∵正方形ABCD的边长为1，BM＝x，

∴AM＝，

∵点N是AM的中点，

∴AN＝，

∵EF⊥AM，

∴∠ANE＝90°，

∴∠ANE＝∠ABM＝90°，

∵∠EAN＝∠MAB，

∴△AEN∽△AMB，

∴＝，即＝，

∴AE＝，

故答案为：；

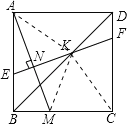
（2）解：如图，连接AK、MG、CK，

由正方形的轴对称性△ABK≌△CBK，

∴AK＝CK，∠KAB＝∠KCB，

∵EF⊥AM，N为AM中点，

∴AK＝MK，

∴MK＝CK，∠KMC＝∠KCM，

∴∠KAB＝∠KMC，

∵∠KMB+∠KMC＝180°，

∴∠KMB+∠KAB＝180°，

又∵四边形ABMK的内角和为360°，∠ABM＝90°，

∴∠AKM＝90°，

在Rt△AKM中，AM为斜边，N为AM的中点，

∴KN＝AM＝AN，

∴＝，

∵△AEN∽△AMB，

∴＝＝x，

∴＝x，

故答案为：x．