题目内容
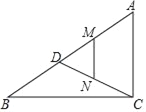
【题目】如图,在![]() 中,
中,![]() 是斜边AB上的中线,以
是斜边AB上的中线,以![]() 为直径的
为直径的![]() 分别交于
分别交于![]() 点
点![]() ,过点N作
,过点N作![]() ,垂足为
,垂足为![]() .
.
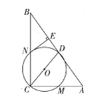
(1)求证:![]() 与
与![]() 相切;
相切;
(2)若![]() 半径为
半径为![]() ,
,![]() ,则
,则![]() 的长为_______________;
的长为_______________;
【答案】(1)证明过程见详解;(2)BN=4
【解析】
(1)连接ON,证明出ON∥AB,ON⊥NE即可.
(2)直角三角形斜边中线等于斜边一半,所以AB=10,由勾股定理求出BC=8,由等腰三角形的性质可知,BN=4.
(1)证明:如图连接ON
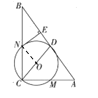
∵∠ACB=![]() ,D为斜边的中点,
,D为斜边的中点,
∴CD=DA=DB=![]() AB
AB
∴∠BCD=∠B
∵OC=ON
∴∠BCD=∠ONC
∴∠ONC=∠B
∴ON∥AB
∵NE⊥AB
∴ON⊥NE
∴NE为圆O的切线.
(2)如图,连接DN
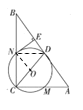
因为圆O的半径为![]() ,
,
∴CD=5
∵∠ACB=![]() ,CD是斜边AB上的中线,
,CD是斜边AB上的中线,
∴BD=CD=AD=5
∴AB=10
∴BC=![]() =8
=8
∵CD为直径,
∴∠CND=![]()
且BD=CD
∴BN=NC=4

练习册系列答案
相关题目