Question

【题目】如图，正方形ABCD中，点E、F分别在边BC、CD上，连接AE、EF、AF，且∠EAF＝45°，下列结论：

①△ABE≌△ADF；

②∠AEB＝∠AEF；

③正方形ABCD的周长＝2△CEF的周长；

④S△ABE+S△ADF＝S△CEF，其中正确的是_____．（只填写序号）

Answer 1

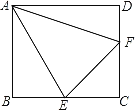
【答案】②③

【解析】

当E、F不是BC和CD的中点时，BE≠DF，则△ABE和△ADF的边对应不相等，由此判断①；延长CD至G，使得DG＝BE，证明△ABE≌△ADG和△AEF≌△AGF，即可判断②；通过周长公式计算，再由BE+DF＝EF，即可判断③；证明S△ABE+S△ADF＝S△AGF，再由三角形的底与高的数量关系得S△AGF＞S△CEF，进而判断④．

解：①当E、F不是BC和CD的中点时，BE≠DF，则△ABE≌△ADF不成立，故①错误；

②延长CD至G，使得DG＝BE，连接AG，如图1，

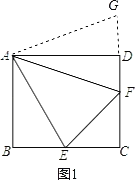
∵四边形ABCD为正方形

∴AB＝AD，∠ABE＝∠ADG＝90°，

∴△ABE≌△ADG（SAS），

∴∠BAE＝∠DAG，∠AEB＝∠G，AE＝AG，

∵∠BAD＝90°，∠EAF＝45°，

∴∠BAE+∠DAF＝45°，

∴∠GAF＝∠DAG+∠DAF＝45°，

∴∠EAF＝∠GAF，

∵AF＝AF，

∴△AEF≌△AGF（SAS），

∴∠AEF＝∠G，

∴∠AEB＝∠AEF，故②正确；

③∵△AEF≌△AGF，

∴EF＝GF＝DG+DF＝BE+DF，

∴△CEF的周长＝CE+CF+EF＝CE+CF+BE+DF＝BC+CD＝2BC，

∵正方形ABCD的周长＝4BC，

∴正方形ABCD的周长＝2△CEF的周长，故③正确；

④∵△ABE≌△ADG，

∴S△ABE＝S△ADG，

∴S△ABE+S△ADF＝S△AGF，

∵GF＝EF＞CF，AD≥CE，

∴，即S△AGF＞S△CEF，

∴S△ABE+S△ADF≠S△CEF，故④错误；

故答案为：②③．