题目内容
【题目】定义:二元一次不等式是指含有两个未知数(即二元),并且未知数的次数是1次(即一次)的不等式;满足二元一次不等式(组)的x和y的取值构成有序数对(x,y),所有这样的有序数对(x,y)构成的集合称为二元一次不等式(组)的解集.如:x+y>3是二元一次不等式,(1,4)是该不等式的解.有序实数对可以看成直角坐标平面内点的坐标.于是二元一次不等式(组)的解集就可以看成直角坐标系内的点构成的集合.
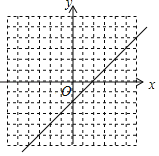
(1)已知A(![]() ,1),B (1,﹣1),C (2,﹣1),D(﹣1,﹣1)四个点,请在直角坐标系中标出这四个点,这四个点中是x﹣y﹣2≤0的解的点是 .
,1),B (1,﹣1),C (2,﹣1),D(﹣1,﹣1)四个点,请在直角坐标系中标出这四个点,这四个点中是x﹣y﹣2≤0的解的点是 .
(2)设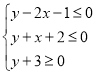 的解集在坐标系内所对应的点形成的图形为G.
的解集在坐标系内所对应的点形成的图形为G.
①求G的面积;
②P(x,y)为G内(含边界)的一点,求3x+2y的取值范围;
(3)设![]() 的解集围成的图形为M,直接写出抛物线y=x2+2mx+3m2﹣m﹣1与图形M有交点时m的取值范围.
的解集围成的图形为M,直接写出抛物线y=x2+2mx+3m2﹣m﹣1与图形M有交点时m的取值范围.
【答案】(1):A、B、D;(2)①3;②﹣12≤3x+2y≤1;(3)0≤m≤![]() .
.
【解析】
(1)在直角坐标系描出A、B、C、D四点,观察图形即可得出结论
(2)①分别画出直线y=2x+1、y=-x-2、y=-3得出图形为G,从而求出G的面积;
②根据P(x,y)为G内(含边界)的一点,求出x、y的范围,从而3x+2y的取值范围;
(3)分别画出直线y=2x+1、y=2x-1、y=-2x-1、y=-2x+1所围成的图形M,再根据抛物线的对称轴x=﹣m,和抛物线y=x2+2mx+3m2﹣m﹣1与图形M有交点,从而求出m的取值范围
解:(1)如图所示:
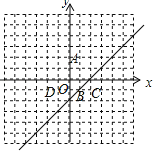
这四个点中是x﹣y﹣2≤0的解的点是A、B、D.
故答案为:A、B、D;
(2)①如图所示:
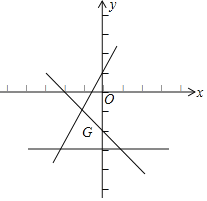
不等式组在坐标系内形成的图形为G,
所以G的面积为:![]() ×3×2=3.
×3×2=3.
②根据图象得:
﹣2≤x≤1,﹣3≤y≤﹣1,
∴﹣6≤3x≤3,﹣6≤2y≤﹣2,
∴﹣12≤3x+2y≤1.
答:3x+2y的取值范围为﹣12≤3x+2y≤1.
(3)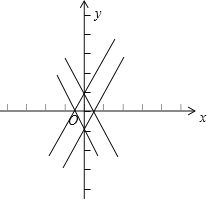
如图所示为
不等式组![]() 的解集围成的图形,设为M,
的解集围成的图形,设为M,
抛物线y=x2+2mx+3m2﹣m﹣1与图形M有交点时m的取值范围:
∵抛物线的对称轴x=﹣m,
﹣m≥﹣![]() ,或﹣m≤
,或﹣m≤![]() ,
,
∴m![]() 或m≥﹣
或m≥﹣![]() .
.
又﹣1≤3m2﹣m﹣1≤1,
∴0≤m≤![]() ,
,
综上:m的取值范围是0≤m≤![]()

【题目】某学校开展了主题为“垃圾分类,绿色生活新时尚”的宣传活动,为了解学生对垃圾分类知识的掌握情况,该校环保社团成员在校园内随机抽取了部分学生进行问卷调查,将他们的得分按优秀、良好、合格、不合格四个等级进行统计,并绘制了如下不完整的统计表和条形统计图.
等级 | 频数 | 频率 |
优秀 | 20 |
|
良好 | ||
合格 | 10 |
|
不合格 | 5 |
|
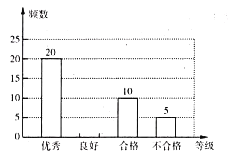
请根据以上信息,解答下列问题:
(1)本次调查随机抽取了______名学生;表中![]() ______,
______,![]() ______;
______;
(2)补全条形统计图;
(3)若全校有2000名学生,请你估计该校掌握垃圾分类知识达到“优秀”和“良好”等级的学生共有多少人.