题目内容
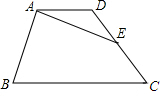
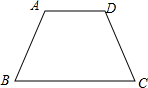
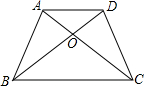
如图,小区的一角有一块形状为等腰梯形的空地,为了美化小区,社区居委会计划在空地上建一个四边形的水池,使水池的四个顶点恰好在梯形各边的中点上,则水池的形状一定是( )

| A.等腰梯形 | B.矩形 | C.菱形 | D.正方形 |

如图,连接对角线AC、BD.
∵点E为AD的中点,点F为AB的中点,
∴EF=
BD,同理可得:GH=
BD,FG=
AC,EH=
AC,
又等腰梯形的对角线相等,即AC=BD,
∴EF=GH=FG=EH,
所以连接各边中点的四边形是菱形.
故选C.
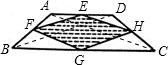
∵点E为AD的中点,点F为AB的中点,
∴EF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又等腰梯形的对角线相等,即AC=BD,
∴EF=GH=FG=EH,
所以连接各边中点的四边形是菱形.
故选C.


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目