题目内容
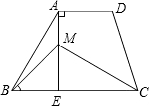
如图，梯形ABCD中，AD∥BC，E是CD的中点，EA⊥AB，且AB=8，AE=6，则梯形ABCD的面积等于（ ）
| A．12 | B．24 | C．48 | D．96 |
如图，延长AE交BC的延长线于F，
∵AD∥BC，
∴∠D=∠ECF，
∵E是CD的中点，
∴DE=CE，
∵在△ADE和△FCE中，
，
∴△ADE≌△FCE（ASA），
∴EF=AE，
∴AF=AE+EF=6+6=12，
∵EA⊥AB，
∴△ABF的面积=
AB•AF=
×8×12=48，
∴梯形ABCD的面积等于48．
故选C．
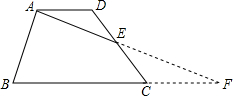
∵AD∥BC，
∴∠D=∠ECF，
∵E是CD的中点，
∴DE=CE，
∵在△ADE和△FCE中，
|
∴△ADE≌△FCE（ASA），
∴EF=AE，
∴AF=AE+EF=6+6=12，
∵EA⊥AB，
∴△ABF的面积=
| 1 |
| 2 |
| 1 |
| 2 |
∴梯形ABCD的面积等于48．
故选C．
练习册系列答案
名校课堂系列答案
相关题目
