Question

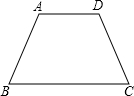
如图，在梯形ABCD中，AD∥BC，AB=DC，AB∥DE，AF∥DC，E，F两点在边BC上．
（1）若AE∥DF，如图1，则四边形AEFD是否是矩形？请说明理由．
（2）若AB=AD，∠B=40°，如图2，求∠EAF的度数．

Answer 1

（1）四边形AEFD为矩形，
证明：∵AD∥BC，AE∥DF，
∴四边形AEFD为平行四边形，
又AD∥BC，AB∥DE，∴四边形ABED为平行四边形，
∴AB=DE，
∵AD∥BC，AF∥DC，∴四边形AFCD为平行四边形，
∴CD=AF，
又AB=CD，∴DE=AF，
∴四边形AEFD为矩形；

（2）由（1）得四边形ABED为平行四边形，
∴AD=BE，又AD=AB，
∴BE=AB，又∠B=40°，
∴∠BAE=∠BEA=

180°-∠B

2

=70°，
由四边形ABCD是梯形且AB=CD，即四边形ABCD为等腰梯形，
∴∠C=∠B=40°，
又AF∥DC，∴∠AFE=∠C=40°，
则∠EAF=∠BEA-∠AFE=30°．