题目内容
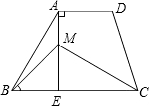
如图，AD∥BC，∠A=90°，BC=BD，CE⊥BD．
（1）求证：CE=AB；
（2）AB=m，AD=n，求tan∠DBC值（用含m、n来表示）．
（1）求证：CE=AB；
（2）AB=m，AD=n，求tan∠DBC值（用含m、n来表示）．
（1）证明：∵AD∥BC，
∴∠1=∠2，
∵CE⊥BD，
∴∠BEC=90°，
∴∠BEC=∠A=90°，
在△ABD和△ECB中，
∵
，
∴△ABD≌△ECB（AAS），
∴CE=AB；
（2）∵AB=m，AD=n，∠A=90°，
∴tan∠1=
=
，
由（1）可知，∠1=∠DBC，
∴tan∠DBC=tan∠1=
．
∴∠1=∠2，
∵CE⊥BD，
∴∠BEC=90°，
∴∠BEC=∠A=90°，
在△ABD和△ECB中，
∵
|
∴△ABD≌△ECB（AAS），
∴CE=AB；
（2）∵AB=m，AD=n，∠A=90°，
∴tan∠1=
| AB |
| AD |
| m |
| n |
由（1）可知，∠1=∠DBC，
∴tan∠DBC=tan∠1=
| m |
| n |
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
品学双优卷系列答案
相关题目
