题目内容
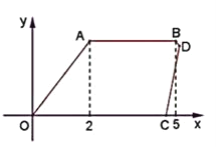
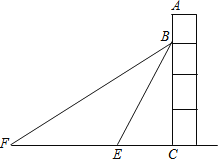
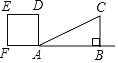
【题目】如图,Rt△ABC中,AB=4,BC=2,正方形ADEF的边长为2,F、A、B在同一直线上,正方形ADEF向右平移到点F与B重合,点F的平移距离为x,平移过程中两图重叠部分的面积为y,则y与x的关系的函数图象表示正确的是( )
A.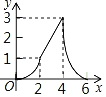 B.
B.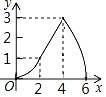
C.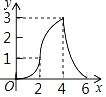 D.
D.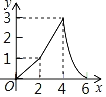
【答案】B
【解析】
分三种情况当0<x≤2时,平移过程中两图重叠部分为Rt△AA'M;当2<x≤4时,平移过程中两图重叠部分为梯形F'A'MN;当4<x≤6时,平移过程中两图重叠部分为梯形F'BCN.分别写出每一部分的函数解析式,结合排除法,问题可解.
设AD交AC于N,![]() 交AC于M,
交AC于M,
当0<x≤2时,平移过程中两图重叠部分为Rt△AA'M,

∵Rt△ABC中,AB=4,BC=2,正方形ADEF的边长为2,
![]() ,
,
∴tan∠CAB=![]() ,
,
∴A'M=![]() x,
x,
其面积y=![]() =
=![]() x
x![]() x=
x=![]() x2,
x2,
故此时y为x的二次函数,排除选项D;
当2<x≤4时,平移过程中两图重叠部分为梯形F'A'MN,
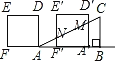
![]() ,
,![]() ,
,
同理:A'M=![]() x,
x,![]() ,
,
其面积y=![]() -
-![]() =
=![]() x
x![]() x﹣
x﹣![]() (x﹣2)
(x﹣2)![]() (x﹣2)=x﹣1,
(x﹣2)=x﹣1,
故此时y为x的一次函数,故排除选项C.
当
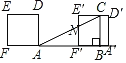
AF'=x﹣2,F'N=![]() (x﹣2),F'B=4﹣(x﹣2)=6﹣x,BC=2,
(x﹣2),F'B=4﹣(x﹣2)=6﹣x,BC=2,
其面积y=![]() [
[![]() (x﹣2)+2]×(6﹣x)=﹣
(x﹣2)+2]×(6﹣x)=﹣![]() x2+x+3,
x2+x+3,
故此时y为x的二次函数,其开口方向向下,故排除A;
综上,只有B符合题意.
故选:B.

练习册系列答案
相关题目