Question

【题目】在Rt△ABC中，AC=3，BC=4，点P是斜边AB上一点，若△PAC是等腰三角形，则线段AP的长可能为____．

Answer 1

【答案】3，2.5或．

【解析】

分三种情况讨论，再利用等腰三角形的性质进行计算即可．

若△PAC是等腰三角形，则分以下三种情况：

①PA=AC=3；

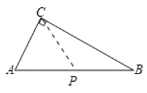
②AP=PC时，则∠A=∠ACP，

∵∠A+∠B=90°，∠ACP+∠BCP=90°，

∴∠B=∠BCP，

∴PC=PB，

∴AP=PB=PC，

∴P为AB的中点，

∵在Rt△ABC中，，

∴AP=2.5；

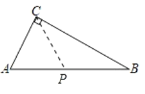
③PC=AC时，过C作CD⊥AB于D，则AP=2AD，

∵在Rt△ACD中，AD=ACcosA，

∴AP=2ACcosA，

又∵在Rt△ABC中，，

∴，

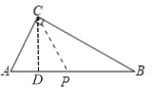
综上所述，AP的长为3，2.5或．

故答案为：3，2.5或．