题目内容
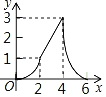
【题目】星期天,小强骑自行车到效外与同学一起游玩.从家出发2小时到达目的地,游玩3小时后按原路以原速返回,小强离家4小时40分钟后,妈妈驾车沿相同路线迎接小强,如图是他们离家的路程y(千米)与时间x(时)的函数图象.已知小强骑车的速度为15千米/时,妈妈驾车的速度为60千米/时.
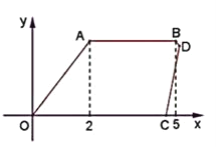
(1)小强家与游玩地的距离是多少?
(2)妈妈出发多长时间与小强相遇?
【答案】(1)30千米;(2) ![]() 小时(或28分钟)
小时(或28分钟)
【解析】
(1)利用路程=速度×时间计算即可;
(2)先利用待定系数法分别求出直线CD、BD的解析式,联立方程组即可求得交点横坐标,即为相遇的时间,减去妈妈出发时小强离家的时间即为所求.
解:(1)小强家与游玩地的距离是15×2=30,
即小强家与游玩地的距离为30千米;
(2)∵小强骑车的速度为15千米/时,妈妈驾车的速度为60千米/时.
∴设yOA=15x,yBD=﹣15x+b1,yCD=60x+b2,
∵点B(5,30),点C(![]() ,0),
,0),
则30=﹣15×5+b1,
解得b1=105,
0=60×![]() +b2,
+b2,
解得b2=﹣280,
则yBD=﹣15x+105,yCD=60x﹣280,相遇即为﹣15x+105=60x﹣280,
解得x=5![]() ,
,
5![]() ﹣4
﹣4![]() =
=![]() 小时(即28分钟).
小时(即28分钟).
或设妈妈出发x时间与小强相遇,则
60x+15(x﹣![]() )=30,
)=30,
解得x=![]() (即28分钟).
(即28分钟).
即妈妈出发28分钟与小强相遇.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目