题目内容
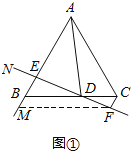
【题目】如图，在等边△ABC中，点D在直线BC上，连接AD，作∠ADN=60°，直线DN交射线AB于点E，过点C作CF∥AB交直线DN于点F．
（1）当点D在线段BC上，∠NDB为锐角时，如图①，
①判断∠1与∠2的大小关系，并说明理由；
②过点F作FM∥BC交射线AB于点M，求证：CF+BE=CD；
（2）当点D在线段BC的延长线上，∠NDB为锐角时，如图②；
当点D在线段CB的延长线上，∠NDB为钝角时，如图③；
请分别写出线段CF，BE，CD之间的数量关系，不需要证明；
（3）在（2）的条件下，若∠ADC=30°，S△ABC=4
，直接写出BE和CD的长度．
【答案】（1）见解析；（2）CF﹣CD=BE；（3）BE=8，CD=4或8．
【解析】
试题分析：（1）①根据等边三角形的性质∠ABC=∠ACB=60°，根据已知条件得到∠1+∠ADC=120°，∠ADC+∠2=120°，根据等式的性质即可得到结论；②通过△MEF≌△CDA即可求得ME=CD，因为通过证四边形BCFM是平行四边形可以得出BM=CF，从而证得CF+BE=CD；
（2）作FM∥BC，得出四边形BCFM是平行四边形，然后通过证得△MEF≌△CDA即可求得，
（3）根据△ABC的面积可求得AB=BC=AC=4，同时代的BD=2AB=8，求得 BE=8，即可得到结论．
解：（1）①∠1=∠2，
∵△ABC是等边三角形，
∴∠ABC=∠ACB=60°
∵∠ADN=60°，
∴∠1+∠ADC=120°，∠ADC+∠2=120°，
∴∠1=∠2；
②证明：如图①，过点F作FM∥BC交射线AB于点M，
∵CF∥AB，
∴四边形BMFC是平行四边形，
∴BC=MF，CF=BM，
∴∠ABC=∠EMF，∠BDE=∠MFE，
∵△ABC是等边三角形，
∴∠ABC=∠ACB=60°，BC=AC，
∴∠EMF=∠ACB，AC=MF，
∵∠ADN=60°，
∴∠BDE+∠ADC=120°，∠ADC+∠DAC=120°，
∴∠BDE=∠DAC，
∴∠MFE=∠DAC，
在△MEF与△CDA中，
，
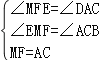∴△MEF≌△CDA（AAS），
∴CD=ME=EB+BM，
∴CD=BE+CF；
（2）如图②，由（1）证得四边形BMFC是平行四边形，
∴BC=MF，CF=BM，
由（1）证得△MEF≌△CDA（AAS），
∴CD=ME=EB﹣BM，
∴CF+CD=BE，
如图③，同理CF﹣CD=BE；
（3）∵△ABC是等边三角形，S△ABC=4
，
∴易得AB=BC=AC=4，
如图②，
∵∠ADC=30°，∠ACB=60°，
∴CD=AC=4，
∵∠ADN=60°，
∴∠CDF=30°，
又∵CF∥AB，
∴∠BCF=∠ABC=60°，
∴∠CFD=∠CDF=30°，
∴CD=CF，
由（2）知BE=CF+CD，
∴BE=4+4=8．
如图③，
∵∠ADC=30°，∠ABC=60°，
∴∠BAD=∠ADC=30°，
∴BD=BA=4，
∴CD=BD+BC=4+4=8，
∵∠ADN=60°，∠ADC=30°，
∴∠BDE=90°，
又∵∠DBE=∠ABC=60°，
∴∠DEB=30°，
在Rt△BDE中，∠DEB=30°，BD=4，
∴BE=2BD=8，
综上，BE=8，CD=4或8．
