题目内容
【题目】三角形内角和定理告诉我们:三角形三个内角的和等于180°.如何证明这个定理呢?
我们知道,平角是180°,要证明这个定理就是把三角形的三个内角转移到一个平角中去,请根据如下条件,证明定理.
(定理证明)
已知:△ABC(如图①).
求证:∠A+∠B+∠C=180°.
(定理推论)如图②,在△ABC中,有∠A+∠B+∠ACB=180°,点D是BC延长线上一点,由平角的定义可得∠ACD+∠ACB=180°,所以∠ACD= .从而得到三角形内角和定理的推论:三角形的外角等于与它不相邻的两个内角的和.
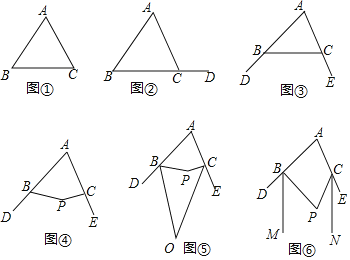
(初步运用)如图③,点D、E分别是△ABC的边AB、AC延长线上一点.
(1)若∠A=80°,∠DBC=150°,则∠ACB= ;
(2)若∠A=80°,则∠DBC+∠ECB= .
(拓展延伸)如图④,点D、E分别是四边形ABPC的边AB、AC延长线上一点.
(1)若∠A=80°,∠P=150°,则∠DBP+∠ECP= ;
(2)分别作∠DBP和∠ECP的平分线,交于点O,如图⑤,若∠O=50°,则∠A和∠P的数量关系为 ;
(3)分别作∠DBP和∠ECP的平分线BM、CN,如图⑥,若∠A=∠P,求证:BM∥CN.
【答案】[定理证明]证明见解析;[定理推论] ∠A+∠ABC; [初步运用](1)70°;(2)260°;[拓展延伸](1)230°;(2)(2)∠P=∠A+100°.(3)证明见解析.
【解析】
[定理证明]
过点A作直线MN∥BC,根据平行线的性质和平角的定义可得结论;
[定理推论]
根据三角形的内角和定理和平角的定义可得结论;
[初步运用]
(1)根据三角形的外角等于与它不相邻的两个内角的和列式可得结论;
(2)根据三角形的内角和得:∠ABC+∠ACB=100°,由两个平角的和可得结论;
[拓展延伸]
(1)连接AP,根据三角形内角和定理的推论可得等式,将两个等式相加可得结论;
(2)如图⑤,设∠DBO=x,∠OCE=y,则∠DBO=∠OBP=x,∠PCO=∠OCE=y,由(1)同理得:x+y=∠A+∠O,2x+2y=∠A+∠P,综合可得结论;
(3)如图⑥,作辅助线,构建三角形PQC,根据(1)的结论得:∠DBP+∠ECP=∠A+∠BPC,和角平分线的定义,证明∠MBP=∠PQC,可得结论.
[定理证明]
证明:过点A作直线MN∥BC,如图所示,
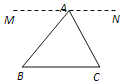
∴∠MAB=∠B,∠NAC=∠C,
∵∠MAB+∠BAC+∠NAC=180°,
∴∠BAC+∠B+∠C=180°;
[定理推论]
∵∠ACD+∠ACB=180°,∠A+∠B+∠ACB=180°,
∴∠ACD=∠A+∠ABC,
故答案为:∠A+∠ABC;
[初步运用]
(1)∵∠DBC=∠A+∠ACB,
∴∠ACB=∠DBC-∠A=150°-80°=70°,
故答案为:70°;
(2)∵∠A=80°,
∴∠ABC+∠ACB=100°,
∴∠DBC+∠ECB=360°-100°=260°,
故答案为:260°;
[拓展延伸]
(1)如图④,连接AP,
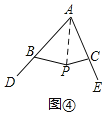
∵∠DBP=∠BAP+∠APB,∠ECP=∠CAP+∠APC,
∴∠DBP+∠ECP=∠BAP+∠APB+∠CAP+∠APC=∠BAC+∠BPC,
∵∠BAC=80°,∠P=150°,
∴∠DBP+∠ECP=∠BAC+∠BPC=80°+130°=230°,
故答案为:230°;
(2)∠P=∠A+100°.
理由是:如图⑤,设∠DBO=x,∠OCE=y,则∠DBO=∠OBP=x,∠PCO=∠OCE=y,
由(1)同理得:x+y=∠A+∠O,2x+2y=∠A+∠P,
2∠A+2∠O=∠A+∠P,
∵∠O=50°,
∴∠P=∠A+100°,
故答案为:∠P=∠A+100°;
(3)证明:延长BP交CN于点Q,
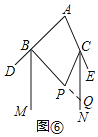
∵BM平分∠DBP,CN平分∠ECP,
∴∠DBP=2∠MBP,∠ECP=2∠NCP,
∵∠DBP+∠ECP=∠A+∠BPC,
∠A=∠BPC,
∴2∠MBP+2∠NCP=∠A+∠BPC=2∠BPC,
∴∠BPC=∠MBP+∠NCP,
∵∠BPC=∠PQC+∠NCP,
∴∠MBP=∠PQC,
∴BM∥CN.