题目内容
【题目】在Rt![]() 中,
中,![]() ,AB=BC,F为AB上一点,连接CF,过B作BH⊥CF于G,交AC于H.
,AB=BC,F为AB上一点,连接CF,过B作BH⊥CF于G,交AC于H.
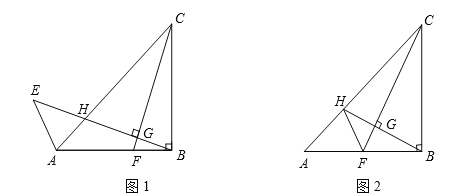
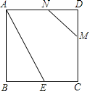
(1)如图1,延长GH到点E,使GE=GC,连接AE,求![]() 的度数;
的度数;
(2)如图2,若F为AB中点,连接FH,请探究BH、FH、CF的数量关系,并证明你的结论.
【答案】(1)![]() ;(2)BH+HF=CF,理由见解析
;(2)BH+HF=CF,理由见解析
【解析】
(1)过点A作AP⊥AB于点P,先找条件证明△ABP≌△BCG,根据对应边相等,以及边的关系,得到PE=PA,又AP⊥PE,得到△APE是等腰直角三角形,即可得到∠E的度数;
(2)过点A作AK⊥AB交BH的延长线于点K,推出Rt△BAK≌Rt△CBF,根据全等三角形的性质得到AK=BF,BK=CF.由F为AB的中点,得到AF=BF,等量代换得到AK=AF,证得△AHK≌△AHF,得到KH=FH.根据线段的和差即可得到结论;
(1)解:过点A作AP⊥AB于点P.
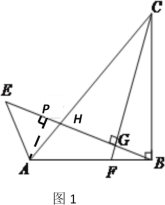
∵BH⊥CF,
∴∠APB=∠CGB=90°,
∵![]() ,
,
∴∠ABP+∠GBC=∠CBG+∠GBC=90°,
∴∠ABP=∠CBG,
在△ABP与△BCG中,
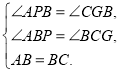
∴△ABP≌△BCG(AAS),
∴BP=CG,AP=BG,
∵GE=GC,
∴BP=GE,
∴PE=BG,
∴PE=PA,
又∵![]()
∴△APE是等腰直角三角形,![]() .
.
(2)解:BH+HF=CF,理由如下:
过点A作AK⊥AB交BH的延长线于点K.
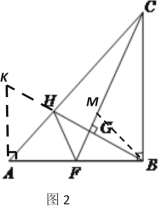
∴∠BAK=∠CBF=90°,
∴∠K+∠ABK=∠CFB+∠ABK=90°,
∴∠K=∠CFB,
在△ABK与△BCF中,
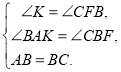 ,
,
∴△ABK≌△BCF(AAS),
∴AK=BF,BK=CF.
∵F为AB的中点,
∴AF=BF,
∴AK=AF,
又∵△APE是等腰直角三角形, ![]() .
.
∴∠HAK=∠HAF![]()
在△AKH与△AFH中,
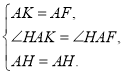
∴△AKH≌△AFH(SAS),
∴HK=HF,
∴BH+HF=BH+HK=BK=CF.

 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案