题目内容
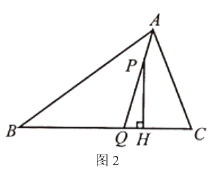
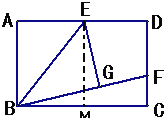
【题目】矩形ABCD中,E是AD的中点,将△ABE折叠后得到△GBE,BG延长交DC于点F,CF=1,FD=2,则BC的长为 .

【答案】2![]() .
.
【解析】
试题此题考查了矩形的判定与性质、折叠的性质、三角形中位线的性质以及全等三角形的判定与性质.此题难度适中,注意辅助线的作法,注意数形结合思想的应用.首先过点E作EM⊥BC于M,交BF于N,易证得△ENG≌△BNM(AAS),MN是△BCF的中位线,根据全等三角形的性质,即可求得GN=MN,由折叠的性质,可得BG=3,继而求得BF的值,又由勾股定理,即可求得BC的长.
解:过点E作EM⊥BC于M,交BF于N,
∵四边形ABCD是矩形,
∴∠A=∠ABC=90°,AD=BC,
∵∠EMB=90°,
∴四边形ABME是矩形,
∴AE=BM,
由折叠的性质得:AE=GE,∠EGN=∠A=90°,
∴EG=BM,
在△ENG和△BNM中
∵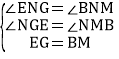 ,
,
∴△ENG≌△BNM(AAS),
∴NG=NM,
∴CM=DE,
∵E是AD的中点,
∴AE=ED=BM=CM,
∵EM∥CD,
∴BN:NF=BM:CM,
∴BN=NF,
∴NM=![]() CF=
CF=![]() ,
,
∴NG=![]() ,
,
∵BG=AB=CD=CF+DF=3,
∴BN=BG-NG=3-![]() =
=![]() ,
,
∴BF=2BN=5,
∴BC=BF2CF2=![]() =2
=2![]() .
.
故答案为:2![]() .
.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目