题目内容
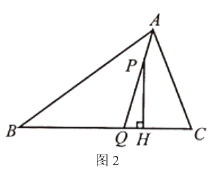
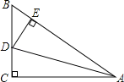
【题目】如图，在△ABC中，∠C=90°，AD平分∠BAC，DE⊥AB于E，则下列结论.①AD平分∠CDE；②∠BAC=∠BDE；③DE平分∠ADB；④BE+AC=AB，其中正确的是____________
【答案】①②④
【解析】
根据题中条件，结合图形及角平分线的性质得到结论，与各选项进行比对，排除错误答案，选出正确的结果．
∵AD平分∠BAC
∴∠DAC=∠DAE
∵∠C=90°，DE⊥AB
∴∠C=∠E=90°
∵AD=AD
∴△DAC≌△DAE
∴∠CDA=∠EDA
∴①AD平分∠CDE正确；
根据已知条件无法证明∠BDE=∠ADE，
∴③DE平分∠ADB错误；
∵BE+AE=AB，AE=AC
∴BE+AC=AB
∴④BE+AC=AB正确；
∵∠BDE=90°∠B,∠BAC=90°∠B
∴∠BDE=∠BAC
∴②∠BAC=∠BDE正确.
练习册系列答案
阅读快车系列答案
相关题目
