题目内容
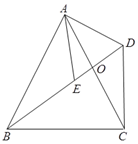
【题目】如图,四边形ABCD中,对角线AC、BD交于点O,AB=AC,点E是BD上一点,且AE=AD,∠EAD=∠BAC.
⑴ 求证:∠ABD=∠ACD;
⑵ 若∠ACB=65°,求∠BDC的度数.
【答案】(1)见解析;(2) 50°
【解析】(1)关键全等三角形的判定与性质证明即可;(2)利用三角形的外角性质和三角形的内角和解答即可.
详解:⑴∵ ∠BAC=∠EAD
∴ ∠BAC-∠EAC=∠EAD-∠EAC
即:∠BAE=∠CA,
在△ABE和△ACD中
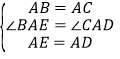
∴ △ABE≌△ACD,
∴ ∠ABD=∠ACD,
⑵∵ ∠BOC是△ABO和△DCO的外角
∴ ∠BOC=∠ABD+∠BAC,∠BOC=∠ACD+∠BDC
∴ ∠ABD+∠BAC=∠ACD+∠BDC
∵ ∠ABD=∠ACD
∴ ∠BAC=∠BDC,
∵ ∠ACB=65°,AB=AC
∴ ∠ABC=∠ACB=65°,
∴ ∠BAC=180°-∠ABC-∠ACB=180°-65°-65°=50°,
∴ ∠BDC=∠BAC=50°

练习册系列答案
相关题目
【题目】在某项针对18﹣35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当0≤m<5时为A级,5≤m<10时为B级,10≤m<15时为C级,m≥15时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微博条数”的调查,制作图表如下: 18﹣35岁青年人日均发微博条数统计表
m | 频数 | 百分数 |
A级(0≤m<5) | 90 | 0.3 |
B级(5≤m<10) | 120 | a |
C级(10≤m<15) | b | 0.2 |
D级(m≥15) | 30 | 0.1 |
请你根据以上信息解答下列问题:
(1)求a,b;
(2)补全频数分布直方图.