题目内容
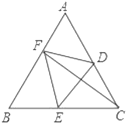
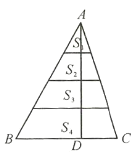
【题目】如图,将![]() 的高
的高![]() 四等分,过每一个等分点作底边的平行线,把三角形的面积分成四部分
四等分,过每一个等分点作底边的平行线,把三角形的面积分成四部分![]() 、
、![]() 、
、![]() 、
、![]() ,则
,则![]() 等于______.
等于______.
【答案】![]()
【解析】
由△ABC的高AD四等分,可得从上到下三角形△AEF、△AGH、△AMN、△ABC的相似比为1:2:3:4,根据相似三角形面积的比等于相似比的平方,可知从上到下三角形△AEF、△AGH、△AMN、△ABC的面积比为1:4:9:16,即可得把三角形的面积分成四部分S1、S2、S3、S4之比.
解:∵△ABC的高AD四等分,且过每一个分点作底边的平行线,
∴从上到下三角形△AEF、△AGH、△AMN、△ABC的相似比为1:2:3:4,
∴从上到下三角形△AEF、△AGH、△AMN、△ABC的面积比为S△AEF:S△AGH:S△AMN:S△ABC =1:4:9:16,
∵如图S2=S△AGH -S△AEF,S3=S△AMN -S△AGH,S4=S△ABC -S△AMN,
∴S1:S2:S3:S4=1:(4-1):(9-4):(16-9)=1:3:5:7.
故答案为:1:3:5:7.

练习册系列答案
相关题目
【题目】某大学生创业团队抓住商机,购进一批干果分装成营养搭配合理的小包装后出售,每袋成本3元.试销期间发现每天的销售量![]() (袋
(袋![]() 与销售单价
与销售单价![]() (元
(元![]() 之间满足一次函数关系,部分数据如表所示,其中3.5≤x≤5.5.另外每天还需支付其他各项费用80元.
之间满足一次函数关系,部分数据如表所示,其中3.5≤x≤5.5.另外每天还需支付其他各项费用80元.
销售单价 | 3.5 | 5.5 |
销售量 | 280 | 120 |
(1)请求出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)设每天的利润为![]() 元,当销售单价定为多少元时,每天的利润最大?最大利润是多少元?
元,当销售单价定为多少元时,每天的利润最大?最大利润是多少元?