Question

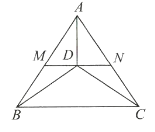
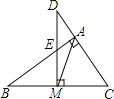
【题目】如图，△ABC中，∠BAC=90°.M为BC的中点，DM⊥BC交CA的延长线于D，交AB于E．求证：

(1)

(2)．

Answer 1

【答案】（1）见解析；（2）见解析.

【解析】

(1)由∠BAC=90°，DM⊥BC可知∠B+∠C=90°，∠C+∠D=90°，即可得∠B=∠D；

(2)利用直角三角形斜边上的中线等于斜边的一半以及等腰三角形的性质得出△AME∽△DMA即可得出答案．

（1）∵∠BAC=90°

∴∠B+∠C=90°，

∵DM⊥BC

∴∠C+∠D=90°，
∴∠B=∠D；

（2）∵∠BAC=90°，M为BC的中点，
∴AM=BM=CM，
∴∠B=∠BAM，
∵∠B+∠C=90°，
∴∠BAM+∠C=90°，
∵∠C+∠D=90°，
∴∠BAM=∠D，
∵∠AME=∠DMA，
∴△AME∽△DMA，
∴，
∴AM2=MDME．