题目内容
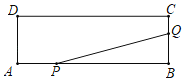
【题目】如图,在等边三角形ABC中,点D、E分别是边AC、BC上两点.将三角形ABC沿DE翻折,点C正好落在线段AB上的点F处,使得AF:BF=2:3.若BE=16,则CE的长度为( )
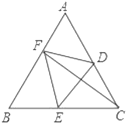
A.18B.19C.20D.21
【答案】B
【解析】
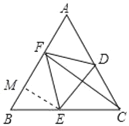
如图,作EM⊥AB于M,由等边三角形的性质可得BC=AB,∠B=60°,可得∠BEM=30°,根据含30°角的直角三角形的性质可求出BM、ME的长,根据折叠的性质可得EF=CE,设EF=CE=x,可用x表示出BC的长,根据AF:BF=2:3可用x表示出BF的长,即可表示出FM的长,在Rt△EFM中,利用勾股定理列方程求出x的值即可得答案.
如图,作EM⊥AB于M,
∵△ABC是等边三角形,
∴BC=AB,∠B=60°,
∵EM⊥AB,
∴∠BEM=30°,
∴BM=![]() BE=8,ME=
BE=8,ME=![]() BM=8
BM=8![]() ,
,
∵三角形ABC沿DE翻折,点C正好落在线段AB上的点F处,
∴FE=CE,
设FE=CE=x,
∴AB=BC=16+x,
∵AF:BF=2:3,
∴BF=![]() (16+x),
(16+x),
∴FM=BF﹣BM=![]() (16+x)﹣8=
(16+x)﹣8=![]() +
+![]() x,
x,
在Rt△EFM中,由勾股定理得:(8![]() )2+(
)2+(![]() x)2=x2,
x)2=x2,
解得:x=19,或x=﹣16(舍去),
∴CE=19.
故选B.

练习册系列答案
相关题目