题目内容
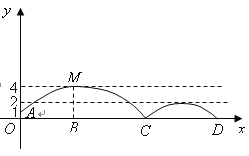
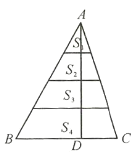
【题目】如图①,![]() 的顶点
的顶点![]() 在正方形
在正方形![]() 两条对角线的交点处,
两条对角线的交点处,![]() ,将
,将![]() 绕点
绕点![]() 旋转,旋转过程中
旋转,旋转过程中![]() 的两边分别与正方形
的两边分别与正方形![]() 的边
的边![]() 和
和![]() 交于点
交于点![]() 和点
和点![]() (点
(点![]() 与点
与点![]() ,
,![]() 不重合).
不重合).
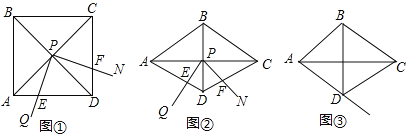
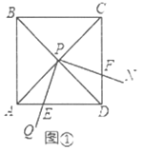
(1)如图①,当![]() 时,求
时,求![]() ,
,![]() ,
,![]() 之间满足的数量关系,并证明;
之间满足的数量关系,并证明;
(2)如图②,将图①中的正方形![]() 改为
改为![]() 的菱形,其他条件不变,当
的菱形,其他条件不变,当![]() 时,(1)中的结论变为
时,(1)中的结论变为![]() ,请给出证明;
,请给出证明;
(3)在(2)的条件下,若旋转过程中![]() 的边
的边![]() 与射线
与射线![]() 交于点
交于点![]() ,其他条件不变,探究在整个运动变化过程中,
,其他条件不变,探究在整个运动变化过程中,![]() ,
,![]() ,
,![]() 之间满足的数量关系,直接写出结论,不用加以证明.
之间满足的数量关系,直接写出结论,不用加以证明.
【答案】(1)![]() ;(2)见解析;(3)当点
;(2)见解析;(3)当点![]() 落在
落在![]() 上时
上时![]() ,当点
,当点![]() 落在
落在![]() 的延长线上时DF-DE=
的延长线上时DF-DE=![]() AD,见解析.
AD,见解析.
【解析】
(1)利用正方形的性质得出角与线段的关系,易证得△APE≌△DPF,可得出AE=DF,即可得出结论DE+DF=AD,
(2)取AD的中点M,连接PM,利用菱形的性质,可得出△MDP是等边三角形,易证△MPE≌△FPD,得出ME=DF,由DE+ME=![]() AD,即可得出DE+DF=
AD,即可得出DE+DF=![]() AD,
AD,
(3))①当点E落在AD上时,DE+DF=![]() AD,②当点E落在AD的延长线上时,DF-DE=
AD,②当点E落在AD的延长线上时,DF-DE=![]() AD.
AD.
解:(1)∵正方形![]() 的对角线
的对角线![]() ,
,![]() 交于点
交于点![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
∴![]() ,
,
∵![]() ,∴
,∴![]()
∴![]() ,
,
∵![]()
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
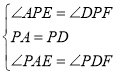
∴![]()
![]()
![]() ,
,
∴![]() ,
,
∴![]() ,
,
(2)方法一:如图②,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
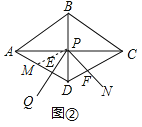
∵四边形![]() 为菱形,
为菱形,
∴![]() ,
,![]() ,
,![]()
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
又∵![]() ,
,
∴![]()
又∵![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,![]()
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
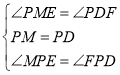
∴![]()
![]()
![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ,
,
方法二:如图②,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
∵四边形![]() 为菱形,
为菱形,
∴![]() ,
,![]()
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴在![]() 中,
中,![]() ,
,
又∵![]() 是
是![]() 的中点,∴
的中点,∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
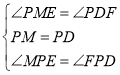
∴![]()
![]()
![]() ,
,
∴![]() ,
,
∴![]() ,
,
(3)
在整个运动变化过程中,
①当点![]() 落在
落在![]() 上时,方法同上可得:
上时,方法同上可得:![]() ,
,
②当点![]() 落在
落在![]() 的延长线上时,取AD中点M,连接PM,
的延长线上时,取AD中点M,连接PM,
如图③,
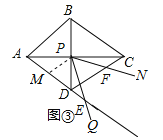
∵四边形ABCD为菱形,∠ADC=120°,
∴AD=CD,∠DAP=30°,AC⊥BD,
∴∠ADP=∠CDP=60°,
∵AM=MD,
∴PM=MD,
∴△MDP是等边三角形,
∴∠PME=∠MPD=60°,PM=PD,
∵∠QPN=60°,
∴∠MPE=∠FPD,
在△MPE和△DPF中,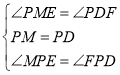
∴△MPE≌△DPF(ASA).
∴ME=DF,
∴DF-DE=![]() AD.
AD.

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案