��Ŀ����
����Ŀ����֪������y��mx2+2mx+n��x���һ������ΪA����3��0������y��ĸ����ύ�ڵ�C��
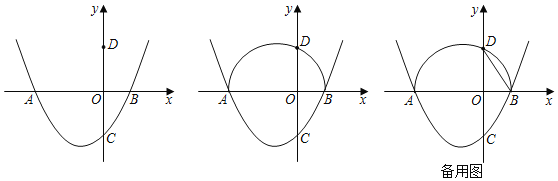
��1��ֱ��д�������ߵĶԳ��ᣬ����������x�����һ������B�����ꣻ
��2����C����x��ĶԳƵ�Ϊ��D������D����ABΪֱ���İ�Բ��ʱ���������ߵĽ���ʽ��
��3���ڣ�2��������£������������Ƿ����һ��P��ʹBP��BD��AB����֮�У�����һ�������������нǵĽ�ƽ���ߣ������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��x����1����B��1��0������2��y��![]() x2+
x2+![]() x��
x��![]() ����3����P����������0����
����3����P����������0����![]() ����4��
����4��![]() ����
����
��������
��1�������ĶԳ���Ϊ��x=-![]() =-1����A��-3��0�������B��1��0����
=-1����A��-3��0�������B��1��0����
��2����BE=ED����4=1+n2����ã�n=-![]() ����ֵ����ȥ�����ʵ�C��0��-
����ֵ����ȥ�����ʵ�C��0��-![]() ����������⣻
����������⣻
��3����AB�ǽ�ƽ���ߡ�BP�ǽ�ƽ���ߡ�BD�ǽ�ƽ��������������ֱ���⼴�ɣ�
��1�������ĶԳ���Ϊ��x����![]() ����1��
����1��
��A����3��0�������B��1��0����
��2����C��0��n�������D��0����n����
��Բ��Բ��ΪE����1��0����
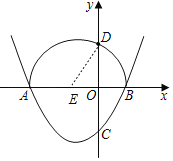
��BE��ED����4��1+n2����ã�n����![]() ����ֵ����ȥ����
����ֵ����ȥ����
�ʵ�C��0����![]() ����
����
�������ߵı���ʽΪ��y��a��x+3����x��1����a��x2+2x��3����
����3a����![]() ����ã�a��
����ã�a��![]() ��
��
�������ߵı���ʽΪ��y��![]() x2+
x2+![]() x��
x��![]() ���٣�
���٣�
��3���ٵ�AB�ǽ�ƽ����ʱ��
���ڵ�D��C����x��Գƣ��ʵ�C��Ϊ��P��0����![]() ����
����
�ڵ�BP�ǽ�ƽ����ʱ��
����OD��![]() ��OB��1���ʡ�DBA��60�㣬��BP����б��Ϊ30�㣬
��OB��1���ʡ�DBA��60�㣬��BP����б��Ϊ30�㣬
��ֱ��BP�ı���ʽΪ��y����![]() x+b������B�����������ʽ����ã�b��
x+b������B�����������ʽ����ã�b��![]() ��
��
��ֱ��BP�ı���ʽΪ��y����![]() x+
x+![]() ���ڣ�
���ڣ�
�����٢ڲ���ã�x����4��1����ȥ1�����ʵ�P����4��![]() ����
����
�۵�BD�ǽ�ƽ����ʱ��
ͬ����P��m��![]() m��
m��![]() ����
����
����P����������ʽ����ã�x��0��1����ȥ����
���ϣ���P������Ϊ����0����![]() ����4��
����4��![]() ����
����