题目内容
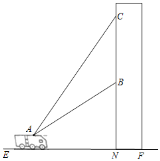
【题目】 如图,某消防队在一居民楼前进行演习,消防员利用云梯成功救出点B处的求救者后,又发现点B正上方点C处还有一名求救者,在消防车上点A处测得点B和点C的仰角分别为45°和65°,点A距地面2.3米,点B距地面10.8米,为救出点C处的求救者,云梯需要继续上升的高度BC约为多少米?结果保留整数,参考数据:tan65°≈2.1,sin65°≈0.9,cos65°≈0.4,![]() ≈1.4)
≈1.4)
【答案】14
【解析】
作AH⊥EF于H,作AD⊥BN于D,则易得四边形AHND为矩形,所以DN=AH=2.3,则BD=8.5,利用∠BAD=45°得到AD=BD=8.5,在Rt△ABD中利用正切值求出CD的长,然后计算CD-BD即可.
作AH⊥EF于H,作AD⊥BN于D,如图,
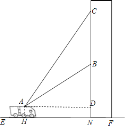
AH=2.3,∠BAD=45°,∠CAD=65°,BN=10.8,易得四边形AHND为矩形,
∴DN=AH=2.3,
∴BD=BN﹣DN=10.8﹣2.3=8.5,
在Rt△ABD中,∵∠BAD=45°,
∴AD=BD=8.5,
在Rt△ABD中,∵tan∠CAD=![]() ,
,
∴CD=10.8tan65°=10.8×2.1=22.68,
∴CB=CD﹣BD=22.68﹣8.5=14.18≈14
答:云梯需要继续上升的高度BC约为14米.

练习册系列答案
相关题目