Question

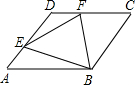
菱形ABCD边长为4，∠BAD=60°，点E是AD上一动点（不与A、D重合），点F是CD上一动点，AE+CF=4，则△BEF面积的最小值为（　　）

A．2 3

B．3 3

C．4 3

D．6 3

Answer 1

∵菱形ABCD边长为4，∠BAD=60°；
∴△ABD与△BCD为正三角形；
∴BD=4，AC=4

3

，△ABE的边AE上的高与_^△BCF的边CF上的高都为2

3

，∠ADC=120；
设AE为x，则CF为4-x；
∴S_△DEF=

1

2

ED•DFsin120°=

1

2

（4-x）[4-（4-x）]

3

2

=-

3

4

x²+

3

x；
由图示可知：S_△BEF=S_菱形ABCD-S_△ABE^--S_△BCF-S_△DEF
=

1

2

×4×4

3

-

3

CF-

3

AE-S_△DEF
=8

3

-

3

（CF+AE）-S_△DEF
=8

3

-4

3

-S_△DEF
=

3

4

x²-

3

x+4

3

；
根据二次函数的性质，△BEF面积的最小值=

-△

4a

=

4× 3 4 ×4 3 -3

3

=

9

3

=3

3

．
故选B．