题目内容
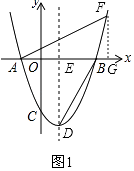
【题目】如图,抛物线y= ![]() x2+bx+c与x轴交于A、B两点,与y轴交于点C,其对称轴交抛物线于点D,交x轴于点E,已知OB=OC=6.
x2+bx+c与x轴交于A、B两点,与y轴交于点C,其对称轴交抛物线于点D,交x轴于点E,已知OB=OC=6.
(1)求抛物线的解析式及点D的坐标;
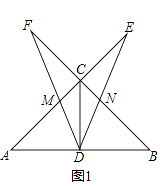
(2)连接BD,F为抛物线上一动点,当∠FAB=∠EDB时,求点F的坐标;
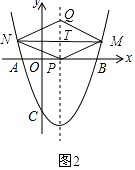
(3)平行于x轴的直线交抛物线于M、N两点,以线段MN为对角线作菱形MPNQ,当点P在x轴上,且PQ= ![]() MN时,求菱形对角线MN的长.
MN时,求菱形对角线MN的长.
【答案】
(1)
解:∵OB=OC=6,
∴B(6,0),C(0,﹣6),
∴ 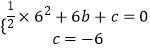 ,解得
,解得 ![]() ,
,
∴抛物线解析式为y= ![]() x2﹣2x﹣6,
x2﹣2x﹣6,
∵y= ![]() x2﹣2x﹣6=
x2﹣2x﹣6= ![]() (x﹣2)2﹣8,
(x﹣2)2﹣8,
∴点D的坐标为(2,﹣8);
(2)
解:如图1,过F作FG⊥x轴于点G,
设F(x, ![]() x2﹣2x﹣6),则FG=|
x2﹣2x﹣6),则FG=| ![]() x2﹣2x﹣6|,
x2﹣2x﹣6|,
在y= ![]() x2﹣2x﹣6中,令y=0可得
x2﹣2x﹣6中,令y=0可得 ![]() x2﹣2x﹣6=0,解得x=﹣2或x=6,
x2﹣2x﹣6=0,解得x=﹣2或x=6,
∴A(﹣2,0),
∴OA=2,则AG=x+2,
∵B(6,0),D(2,﹣8),
∴BE=6﹣2=4,DE=8,
当∠FAB=∠EDB时,且∠FGA=∠BED,
∴△FAG∽△BDE,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() =
= ![]() ,
,
当点F在x轴上方时,则有 ![]() =
= ![]() ,解得x=﹣2(舍去)或x=7,此进F点坐标为(7,
,解得x=﹣2(舍去)或x=7,此进F点坐标为(7, ![]() );
);
当点F在x轴上方时,则有 ![]() =﹣
=﹣ ![]() ,解得x=﹣2(舍去)或x=5,此进F点坐标为(5,﹣
,解得x=﹣2(舍去)或x=5,此进F点坐标为(5,﹣ ![]() );
);
综上可知F点的坐标为(7, ![]() )或(5,﹣
)或(5,﹣ ![]() );
);
(3)
解:∵点P在x轴上,
∴由菱形的对称性可知P(2,0),
如图2,当MN在x轴上方时,设T为菱形对角线的交点,
∵PQ= ![]() MN,
MN,
∴MT=2PT,
设PT=n,则MT=2n,
∴M(2+2n,n),
∵M在抛物线上,
∴n= ![]() (2+2n)2﹣2(2+2n)﹣6,解得n=
(2+2n)2﹣2(2+2n)﹣6,解得n= ![]() 或n=
或n= ![]() ,
,
∴MN=2MT=4n= ![]() +1;
+1;
当MN在x轴下方时,同理可设PT=n,则M(2+2n,﹣n),
∴﹣n= ![]() (2+2n)2﹣2(2+2n)﹣6,解得n=
(2+2n)2﹣2(2+2n)﹣6,解得n= ![]() 或n=
或n= ![]() (舍去),
(舍去),
∴MN=2MT=4n= ![]() ﹣1;
﹣1;
综上可知菱形对角线MN的长为 ![]() +1或
+1或 ![]() ﹣1.
﹣1.
【解析】(1)由条件可求得B、C坐标,利用待定系数法可求得抛物线解析式,进一步可求得D点坐标;(2)过F作FG⊥x轴于点G,可设出F点坐标,利用△FAG∽△BDE,由相似三角形的性质可得到关于F点坐标的方程,可求得F点的坐标;(3)可求得P点坐标,设T为菱形对角线的交点,设出PT的长为n,从而可表示出M点的坐标,代入抛物线解析式可得到n的方程,可求得n的值,从而可求得MN的长.
【考点精析】认真审题,首先需要了解相似三角形的性质(对应角相等,对应边成比例的两个三角形叫做相似三角形).

 名校课堂系列答案
名校课堂系列答案