题目内容
【题目】如图,在△ABC中,∠ACB=90°,CD是中线,AC=BC,一个以点D为顶点的45°角绕点D旋转,使角的两边分别与AC、BC的延长线相交,交点分别为点E,F,DF与AC交于点M,DE与BC交于点N.
(1)如图1,若CE=CF,求证:DE=DF;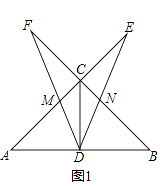
(2)如图2,在∠EDF绕点D旋转的过程中:
①探究三条线段AB,CE,CF之间的数量关系,并说明理由;
②若CE=4,CF=2,求DN的长.
【答案】
(1)
证明:∵∠ACB=90°,AC=BC,AD=BD,
∴∠BCD=∠ACD=45°,∠BCE=∠ACF=90°,
∴∠DCE=∠DCF=135°,
在△DCE与△DCF中,  ,
,
∴△DCE≌△DCF,
∴DE=DF;
(2)
解:①∵∠DCF=∠DCE=135°,
∴∠CDF+∠F=180°﹣135°=45°,
∵∠CDF+∠CDE=45°,
∴∠F=∠CDE,
∴△CDF∽△CED,
∴ ![]() ,
,
即CD2=CECF,
∵∠ACB=90°,AC=BC,AD=BD,
∴CD= ![]() AB,
AB,
∴AB2=4CECF;
②如图,过D作DG⊥BC于G,

则∠DGN=∠ECN=90°,CG=DG,
当CE=4,CF=2时,
由CD2=CECF得CD=2 ![]() ,
,
∴在Rt△DCG中,CG=DG=CDsin∠DCG=2 ![]() ×sin45°=2,
×sin45°=2,
∵∠ECN=∠DGN,∠ENC=∠DNG,
∴△CEN∽△GDN,
∴ ![]() =2,
=2,
∴GN= ![]() CG=
CG= ![]() ,
,
∴DN= ![]() =
= ![]() =
= ![]() .
.
【解析】(1)根据等腰直角三角形的性质得到∠BCD=∠ACD=45°,∠BCE=∠ACF=90°,于是得到∠DCE=∠DCF=135°,根据全等三角形的性质即可的结论;(2)①证得△CDF∽△CED,根据相似三角形的性质得到 ![]() ,即CD2=CECF,根据等腰直角三角形的性质得到CD=
,即CD2=CECF,根据等腰直角三角形的性质得到CD= ![]() AB,于是得到AB2=4CECF;②如图,过D作DG⊥BC于G,于是得到∠DGN=∠ECN=90°,CG=DG,当CE=4,CF=2时,求得CD=2
AB,于是得到AB2=4CECF;②如图,过D作DG⊥BC于G,于是得到∠DGN=∠ECN=90°,CG=DG,当CE=4,CF=2时,求得CD=2 ![]() ,推出△CEN∽△GDN,根据相似三角形的性质得到
,推出△CEN∽△GDN,根据相似三角形的性质得到 ![]() =2,根据勾股定理即可得到结论.
=2,根据勾股定理即可得到结论.
【考点精析】掌握等腰直角三角形和勾股定理的概念是解答本题的根本,需要知道等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案





