题目内容
【题目】如图,正方形ABCD的顶点A,B在函数y= ![]() (x>0)的图象上,点C,D分别在x轴,y轴的正半轴上,当k的值改变时,正方形ABCD的大小也随之改变.
(x>0)的图象上,点C,D分别在x轴,y轴的正半轴上,当k的值改变时,正方形ABCD的大小也随之改变.
①当k=2时,正方形A′B′C′D′的边长等于 .
②当变化的正方形ABCD与(1)中的正方形A′B′C′D′有重叠部分时,k的取值范围是 . 
【答案】![]() ;
;![]() ≤x≤18
≤x≤18
【解析】解:(1)如图,过点A′作AE⊥y轴于点E,过点B′⊥x轴于点F,则∠A′ED′=90°. 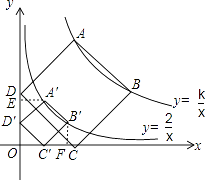
∵四边形A′B′C′D′为正方形,
∴A′D′=D′C′,∠A′D′C′=90°,
∴∠OD′C′+∠ED′A′=90°.
∵∠OD′C′+∠OC′D′=90°,
∴∠ED′A′=∠OC′D′.
在△A′ED′和△D′OC′中,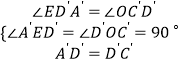 ,
,
∴△A′ED′≌△D′OC′(AAS).
∴OD′=EA′,OC′=ED′.
同理△B′FC′≌△C′OD′.
设OD′=a,OC′=b,则EA′=FC′=OD′=a,ED′=FB′=OC′=b,
即点A′(a,a+b),点B′(a+b,b).
∵点A′、B′在反比例函数y= ![]() 的图象上,
的图象上,
∴ ![]() ,解得:
,解得: ![]() 或
或 ![]() (舍去).
(舍去).
在Rt△C′OD′中,∠C′OD′=90°,OD′=OC′=1,
∴C′D′= ![]() =
= ![]() .
.
所以答案是: ![]() .
.
2)设直线A′B′解析式为y=k1x+b1 , 直线C′D′解析式为y=k2+b2 ,
∵点A′(1,2),点B′(2,1),点C′(1,0),点D′(0,1),
∴有 ![]() 和
和 ![]() ,
,
解得: ![]() 和
和 ![]() .
.
∴直线A′B′解析式为y=﹣x+3,直线C′D′解析式为y=﹣x+1.
设点A的坐标为(m,2m),点D坐标为(0,n).
当A点在直线C′D′上时,有2m=﹣m+1,解得:m= ![]() ,
,
此时点A的坐标为( ![]() ,
, ![]() ),
),
∴k= ![]() ×
× ![]() =
= ![]() ;
;
当点D在直线A′B′上时,有n=3,
此时点A的坐标为(3,6),
∴k=3×6=18.
综上可知:当变化的正方形ABCD与(1)中的正方形A′B′C′D′有重叠部分时,k的取值范围为 ![]() ≤x≤18.
≤x≤18.
所以答案是: ![]() ≤x≤18.
≤x≤18.
【考点精析】关于本题考查的反比例函数的性质和正方形的性质,需要了解性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能得出正确答案.