题目内容
【题目】如图,在正方形ABCD中,点E、F分别在边BC和CD上,且BE=CF,连接AE、BF,其相交于点G,将△BCF沿BF翻折得到△BC′F,延长FC′交BA延长线于点H.
(1)①求证:AE=BF;
②猜想AE与BF的位置关系,并证明你的结论;
(2)若AB=3,EC=2BE,求BH的长.
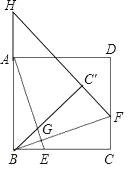
【答案】(1)①详见解析;②AE⊥BF,证明详见解析;(2)BH=5.
【解析】
(1)①根据正方形的性质得到BA=BC,∠ABC=∠BCD=90°,利用SAS证明△ABE≌△BCF,根据全等三角形的性质证明结论;
②根据全等三角形的性质得到∠BAE=∠CBF,根据垂直的定义证明;
(2)根据折叠的性质得到∠C′BF=∠CBF,∠BC′F=∠BCF=90°,证明HB=HF,根据勾股定理列式计算即可.
(1)①证明:∵四边形ABCD是正方形,
∴BA=BC,∠ABC=∠BCD=90°,
在△ABE和△BCF中,
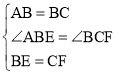 ,
,
∴△ABE≌△BCF(SAS),
∴AE=BF;
②解:AE⊥BF,
理由如下:∵△ABE≌△BCF,
∴∠BAE=∠CBF,
∵∠ABE=90°,
∴∠BAE+∠AEB=90°,
∴∠CBF+∠AEB=90°,即AE⊥BF;
(2)解:∵BC=AB=3,EC=2BE,
∴EC=2,BE=1,
∴C′F=CF=1,
由折叠的性质可知,∠C′BF=∠CBF,∠BC′F=∠BCF=90°,
∵∠C′FB+∠C′BF=90°,∠HBF+∠FBC=90°,
∴∠C′FB=∠HBF,
∴HB=HF,
∴HC′=HF﹣C′F=HB﹣C′F=3+AH﹣1=2+AH,
在Rt△HBC′中,HB2=C′B2+C′H2,即(3+AH)2=32+(2+AH)2,
解得,AH=2,
∴BH=AH+AB=5.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目