Question

【题目】（1）（问题发现）

如图1，△ABC和△ADE都是等腰直角三角形，∠BAC＝∠DAE＝90°，延长CA到点F，使得AF＝AC，连接DF、BE，则线段BE与DF的数量关系为　 　，位置关系为　 　；

（2）（拓展研究）

将△ADE绕点A旋转，（1）中的结论有无变化？仅就图（2）的情形给出证明；

（3）（解决问题）

当AB＝2，AD＝，△ADE旋转得到D，E，F三点共线时，直接写出线段DF的长．

Answer 1

【答案】（1）DF＝BE，DF⊥BE；（2）详见解析；（3）DF＝+1或﹣1

【解析】

（1）通过证明△ABE≌△AFD，可得DF＝BE，DF⊥BE；

（2）通过证明△ADF≌△AEB，可得DF＝BE，DF⊥BE；

（3）分点D在AB左侧和右侧两种情况讨论，由等腰直角三角形的性质和勾股定理可求FH的长，即可求DF的长．

（1）延长FD交BE于点M

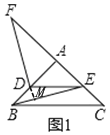
∵△ABC和△ADE都是等腰直角三角形

∴AD＝AE，AB＝AC，∠BAC＝90°＝∠FAD

∵AF＝AC

∴AF＝AB，且AD＝AE，∠BAE＝∠DAF＝90°

∴△ABE≌△AFD（SAS）

∴FD＝BE，∠F＝∠ABE，

∵∠ABE+∠AEB＝90°

∴∠F+∠AEB＝90°

∴∠FME＝90°

∴FD⊥BE

故答案为：DF＝BE，DF⊥BE

【拓展研究】

（2）

∵∠BAC＝90°＝∠EAD

∴∠DAF＝∠EAB＝90°+∠EAF

在△ADF 和△AEB 中

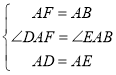
∴△ADF≌△AEB

DF＝BE，∠F＝∠EBA

设 CF 和 BE 相交于点 H，则∠EHF＝∠CHB

∵∠BAC＝∠DAE＝90°

∴∠EBA+∠CHB＝90°

∴∠F+∠EHF＝90°

∴DF⊥BE

（3）当点D在AB的左侧，

如图，过点A作AH⊥EF于点H，

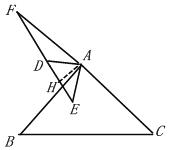
∵△ADE是等腰直角三角形，AD＝AE＝，AH⊥EF

∴DE＝2，AH＝DH＝DE＝1

∵FH＝＝

∴FD＝FH﹣DH＝﹣1

当点D在AB右侧，

如图，过点A作AH⊥EF于点H，

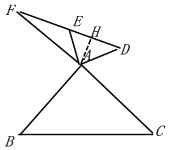
同理可求：FH＝

∴FD＝FH+HD＝+1

综上所述：DF＝+1或﹣1