题目内容
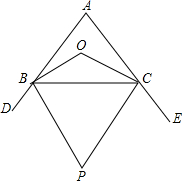
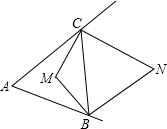
如图，点M是△ABC两个内角平分线的交点，点N是△ABC两个外角平分线的交点，如果∠CMB：∠CNB=3：2，那么∠CAB=______度．
由题意得：∠NCM=∠NBM=
×180°=90°，
∴可得：∠CMB+∠CNB=180°，
又∠CMB：∠CNB=3：2，
∴∠CMB=108°，
∴
（∠ACB+∠ABC）=180°-∠CMB=72°，
∴∠CAB=180°-（∠ACB+∠ABC）=36°．
故答案为：36°．
| 1 |
| 2 |
∴可得：∠CMB+∠CNB=180°，
又∠CMB：∠CNB=3：2，
∴∠CMB=108°，
∴
| 1 |
| 2 |
∴∠CAB=180°-（∠ACB+∠ABC）=36°．
故答案为：36°．
练习册系列答案
全能测控期末小状元系列答案
相关题目
