题目内容
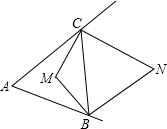
如图,在△ABC中,∠ABC,∠ACB的平分线夹角为α,∠ABC的外角平分线与∠ACB的外角平分线的夹角为β,
(1)若α=110°,则∠A=______.
(2)若∠A=30°,则β=______.
(3)猜想并证明α与β之间的关系.
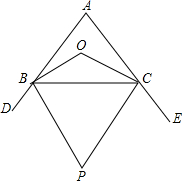
(1)若α=110°,则∠A=______.
(2)若∠A=30°,则β=______.
(3)猜想并证明α与β之间的关系.

(1)∵α=110°,
∴∠2+∠4=180°-110°=70°,
∵∠ABC,∠ACB的平分线夹角为α,
∴∠1=∠2,∠3=∠4,
∴∠1+∠2+∠3+∠4=2(∠2+∠4)=2×70°=140°,
∴∠A=180°-2(∠2+∠4)=180°-140°=40°.
故答案为:40°.
(2)∵∠A=40°,
∴∠ABC+∠ACB=180°-∠A=180°-40°=140°,
∴∠DBC+∠ECB=360°-(∠ABC+∠ACB)=360°-140°=220°,
∵ABC的外角平分线与∠ACB的外角平分线的夹角为β,
∴∠6+∠7=
(∠DBC+∠ECB)=
×220°=110°,
∴β=180°-(∠6+∠7)=180°-110°=70°.
故答案为:70°.
(3)互补.
证明:如图所示:
∵OB,OC分别是∠ABC与∠ACB的平分线,
∴∠1=∠2,3=∠4,
∴α=180°-(∠2+∠4)=180°-
(∠ABC+∠ACB)①;
∵BP,CP是△ABC的外角平分线,
∴∠6+∠7=
[360°-(∠ABC+∠ACB)]=180°-
(∠ABC+∠ACB),
∴β=180°-(∠6+∠7)=180°-180°+
(∠ABC+∠ACB)=
(∠ABC+∠ACB)②,
①+②得,α+β=180°,
∴α与β互补.

∴∠2+∠4=180°-110°=70°,
∵∠ABC,∠ACB的平分线夹角为α,
∴∠1=∠2,∠3=∠4,
∴∠1+∠2+∠3+∠4=2(∠2+∠4)=2×70°=140°,
∴∠A=180°-2(∠2+∠4)=180°-140°=40°.
故答案为:40°.
(2)∵∠A=40°,
∴∠ABC+∠ACB=180°-∠A=180°-40°=140°,
∴∠DBC+∠ECB=360°-(∠ABC+∠ACB)=360°-140°=220°,
∵ABC的外角平分线与∠ACB的外角平分线的夹角为β,
∴∠6+∠7=
| 1 |
| 2 |
| 1 |
| 2 |
∴β=180°-(∠6+∠7)=180°-110°=70°.
故答案为:70°.
(3)互补.
证明:如图所示:
∵OB,OC分别是∠ABC与∠ACB的平分线,
∴∠1=∠2,3=∠4,
∴α=180°-(∠2+∠4)=180°-
| 1 |
| 2 |
∵BP,CP是△ABC的外角平分线,
∴∠6+∠7=
| 1 |
| 2 |
| 1 |
| 2 |
∴β=180°-(∠6+∠7)=180°-180°+
| 1 |
| 2 |
| 1 |
| 2 |
①+②得,α+β=180°,
∴α与β互补.


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目