题目内容
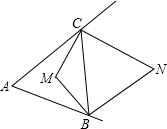
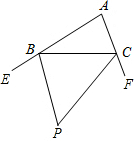
如图所示,在△ABC中,∠A=α,两外角平分线交于P点,∠P=β,则α、β之间的关系为( )

A.β=90°+
| B.β=
| C.β=90°-
| D.α=90°-
|

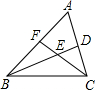
∵BP、CP分别是∠CBE、∠BCF的平分线
∴∠PBC=
∠EBC,∠BCP=
∠BCF,
∵∠CBE、∠BCF是△ABC的两个外角
∴∠CBE+∠BCF=360°-(180°-∠A)=180°+∠A
∴∠PBC+∠BCP=
(∠EBC+∠BCP)=
(180°+∠A)=90°+
∠A,
在△PBC中∠BPC=180°-(∠PBC+∠BCP)=180°-(90°+
∠A)=90°-
∠α.
即β=90°-
α.
故选C.
∴∠PBC=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠CBE、∠BCF是△ABC的两个外角
∴∠CBE+∠BCF=360°-(180°-∠A)=180°+∠A
∴∠PBC+∠BCP=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
在△PBC中∠BPC=180°-(∠PBC+∠BCP)=180°-(90°+
| 1 |
| 2 |
| 1 |
| 2 |
即β=90°-
| 1 |
| 2 |
故选C.


练习册系列答案
相关题目
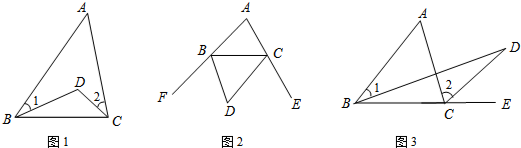
 ,请填空:
,请填空: