题目内容
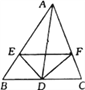
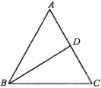
【题目】如图,△ABC中,AB=AC,D为AC的中点,△ABD的周长比△BDC的周长大2,且BC的边长是方程![]() 的解,求△ABC三边的长.
的解,求△ABC三边的长.
【答案】△ABC三边的长为![]()
【解析】
解方程![]() 求解k=4.5,即可得BC=4.5;由D为AC中点可得AD=CD,再由ΔABD的周长比ΔBDC的周长大2,即可得到AB+AD+BD (BC+CD+BD) =2,即ABBC=2,由此求得AB=6.5,即可得AC=6.5,由此问题得解.
求解k=4.5,即可得BC=4.5;由D为AC中点可得AD=CD,再由ΔABD的周长比ΔBDC的周长大2,即可得到AB+AD+BD (BC+CD+BD) =2,即ABBC=2,由此求得AB=6.5,即可得AC=6.5,由此问题得解.
ΔABC的三边长为6.5,6.5,4.5
解方程![]() 得k=4.5,
得k=4.5,
∴BC=4.5,
∵D为AC中点,
∴AD=CD,
∵ΔABD的周长比ΔBDC的周长大2,
∴AB+AD+BD (BC+CD+BD) =2,
即ABBC=2,
∴AB=6.5,
∵AB=AC,
∴AC=6.5,
ΔABC的三边长为6.5,6.5,4.5.

练习册系列答案
相关题目