Question

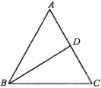
【题目】如图，已知D为△ABC的BC边的中点，DE、DF分别平分∠ADB和∠ADC，

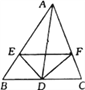
求证：BE＋CF>EF.

Answer 1

【答案】证明见解析.

【解析】

试题分析:在 DA 上取一点 M ，使 DM=DB=DC ，连结 EM 、 MF ，实质上是将△DBE 及△DFC 分别沿 DE 、 DF 翻折 180° 得到△DEM 及△MFD ，从而使问题得到解决的 .

试题解析:在 DA 上取一点 M ，使 DM=DB=DC ，连结 EM 、 MF ，

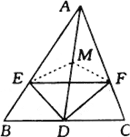
∵ DE 平分∠ADB ，

∴ ∠BDE= ∠EDM.

又∵ DM=BD ， DE=DE ，

∴ △BED ≌△MED.

同理可得△MFD ≌△CFD.

∴ BE=EM ， CF=MF.

∵ 在△EMF 中， EM＋MF>EF.

∴ BE＋CF>EF.