��Ŀ����
����Ŀ����֪����ʽx3��3xy2��3�ij�������a��������b����a=������������b=������������
��������������ͼ��ʾ����������Ӧ�ĵ�A��B��ʾ������
![]()
����̽����
����һ��
(1)�۵�ֽ��,ʹA��ʾ�ĵ���B��ʾ�ĵ��غϣ���5��ʾ�ĵ���__ ___��ʾ�ĵ��غϣ�
�������� (2)�۵�ֽ��,ʹ1��ʾ�ĵ���3��ʾ�ĵ��غϣ��ش��������⣺
��![]() ��ʾ�ĵ�����_____��ʾ�ĵ��غϣ�
��ʾ�ĵ�����_____��ʾ�ĵ��غϣ�
����������C��D����֮�����Ϊ9��(C��D�����)����C��D���㾭�۵����غ�,��C��D�����ʾ�����Ƕ���?
���𰸡�![]() ����1��5����2����-3����C��D�����ʾ�����ֱ���-3.5��5.5.
����1��5����2����-3����C��D�����ʾ�����ֱ���-3.5��5.5.
��������
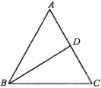
�������Dz�����ĸ�������ʽ�Ĵ����Ƕ���ʽ�д�����ߵ���Ĵ�����
��1��ֱ��������֪�ó��е�����ó��𰸣�
��2��������-1��ʾ�ĵ���3��ʾ�ĵ��غϵó��е㣬�����ó��𰸣�
�����������ٽ����C��D����֮�����Ϊ9�����ɵó������ʾ��������.
�⣺�߲�����ĸ������-3��1+2=3��
���Զ���ʽx3��3xy2��3�ij�����-3��������3��
����a=-3��b=3��
��A��B�������ϱ�ʾ����ͼ��ʾ��

��1���۵�ֽ�棬ʹA��ʾ�ĵ���B��ʾ�ĵ��غϣ���Գ�������0��
��-5��ʾ�ĵ���5��ʾ�ĵ��غϣ�
�ʴ�Ϊ�� 5
��2����-1��ʾ�ĵ���3��ʾ�ĵ��غϣ�
��Գ���������1��ʾ�ĵ㣬
��5��ʾ�ĵ�����-3��ʾ�ĵ��غϣ�
��������ɵã�C��D�������ԳƵ�ľ���Ϊ9��2=4.5���߶ԳƵ��DZ�ʾ1�ĵ㣬
��C��D�����ʾ�����ֱ���-3.5��5.5.