题目内容
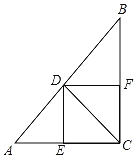
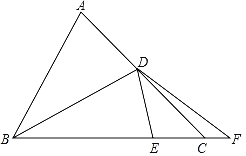
【题目】△ABC中,∠ACB=45°,D为AC上一点,AD=5![]() ,连接BD,将△ABD沿BD翻折至△EBD,点A的对应点E点恰好落在边BC上.延长BC至点F,连接DF,若CF=2,tan∠ABD=
,连接BD,将△ABD沿BD翻折至△EBD,点A的对应点E点恰好落在边BC上.延长BC至点F,连接DF,若CF=2,tan∠ABD=![]() ,则DF长为( )
,则DF长为( )
A.![]() B.
B.![]() C.5
C.5![]() D.7
D.7![]()
【答案】B
【解析】
过![]() 作
作![]() 于
于![]() ,交
,交![]() 于
于![]() ,作
,作![]() 于
于![]() .设
.设![]() ,
,![]() ,由
,由![]() ,可知
,可知![]() .
.
由折叠可知,![]() 平分
平分![]() ,
,![]() ,得
,得![]() ,在
,在![]() 中,
中,![]() ,得出
,得出![]() ,因此
,因此![]() ,
,![]() ,
,![]() ,所以
,所以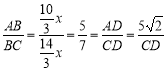 ,
,
得![]() ,
,![]() ,
,![]() ,再由勾股定理
,再由勾股定理![]() .
.
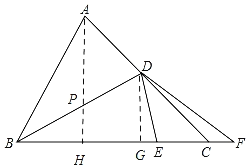
解:如图.过A作AH⊥BC于H,交BD于P,作DG⊥BC于G.
设PH=x,AP=y,
∵tan∠ABD=![]() ,
,
∴BH=2HP=2x.
由折叠可知,BD平分∠ABC,
∴![]() ,
,
∴AB=2y,
在Rt△ABH中,AH2+BH2=AB2,
即,(x+y)2+(2x)2=(2y)2,
∴y=![]() x,
x,
∴AB=![]() ,AH=AP+PH=
,AH=AP+PH=![]() +x=
+x=![]() x,
x,
∵∠ACB=45°,AH⊥BC,
∴CH=AH=![]()
BC=BH+CH=2x+![]() =
=![]() ,
,
∴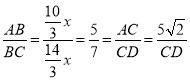 ,
,
∴CD=7![]() ,
,
∴DG=CG=7,
∵CF=2,
∴FG=7+2=9,
∴DF=![]() =
=![]() ,
,
故选:B.

练习册系列答案
相关题目