题目内容
【题目】四边形![]() 是
是![]() 的内接四边形,
的内接四边形,![]() ,
,![]() ,垂足为
,垂足为![]() .
.
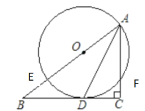
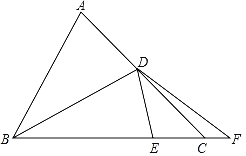
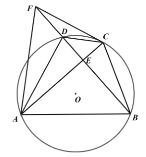
(1)如图1,求证:![]() ;
;
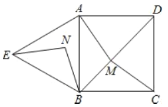
(2)如图2,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,连接
,连接![]() 、
、![]() ,求证:
,求证:![]() ;
;
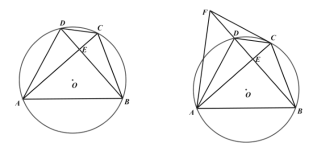
(3)如图3,在(2)的条件下,若![]() ,
,![]() ,求
,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)由圆周角定理得出∠DAC=∠CBD,证出∠ACB=90°∠CBD,由等腰三角形的性质得出∠ABC=∠ACB=90°∠CBD,得出∠BAC=180°2∠ABC=2∠CBD,即可得出结论;
(2)由等腰三角形的性质得出∠FCD=∠CFD,证出∠CFD=∠CAD,进而得出∠CFD=∠CBD,即可得出结论;
(3)证出AB=AF=AC=10设AE=x,CE=10x,由勾股定理得出AB2AE2=BC2CE2,得出102x2=(4![]() )2(10x)2,求出AE=6,CE=4,由勾股定理得出BE=8,由三角函数定义得出
)2(10x)2,求出AE=6,CE=4,由勾股定理得出BE=8,由三角函数定义得出![]() ,求出DE=3,由勾股定理得出AD=3
,求出DE=3,由勾股定理得出AD=3![]() ,过点D作DH⊥AB,垂足为H,由面积法求出DH=
,过点D作DH⊥AB,垂足为H,由面积法求出DH=![]() ,由三角函数定义即可得出答案.
,由三角函数定义即可得出答案.
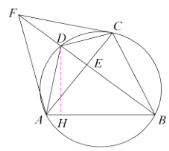
(1)证明:如图1,
∵弧![]() 弧
弧![]()
∴![]()
∵![]() ,
,
∴![]() ,
,
∴![]()
∵![]() ,∴
,∴![]() ,
,
∴![]()
∴![]()
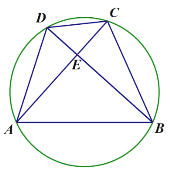
(2)证明:如图2,∵![]()
∴![]()
∴![]()
∴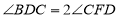
∵![]() ,
,![]()
∴![]()
∵![]()
∴![]()
∴![]()
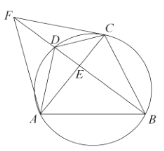
(3)解:如图3,∵![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() 垂直平分
垂直平分![]() ,
,
∴![]()
设![]() ,
,![]() ,
,
在![]() 中,
中,![]()
在![]() 中,
中,![]() ,
,
∴![]() ,∵
,∵![]()
∴![]() ,解得
,解得![]()
∴![]() ,
,![]()
∴![]() ,
,
∵![]() ,
,
∴![]()
∴![]() ,
,
∴![]()
在![]() 中,
中,![]()
∴![]()
过点![]() 作
作![]() ,垂足为
,垂足为![]()
∴![]()
![]()
∴![]()
在![]() 中,
中,
∴![]() .
.

 阅读快车系列答案
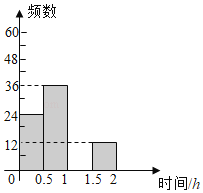
阅读快车系列答案【题目】扬州市“五个一百工程“在各校普遍开展,为了了解某校学生每天课外阅读所用的时间情况,从该校学生中随机抽取了部分学生进行问卷调查,并将结果绘制成如图不完整的频数分布表和频数分布直方图.
每天课外阅读时间t/h | 频数 | 频率 |
0<t≤0.5 | 24 | |
0.5<t≤1 | 36 | 0.3 |
1<t≤1.5 | 0.4 | |
1.5<t≤2 | 12 | b |
合计 | a | 1 |
根据以上信息,回答下列问题:
(1)表中a= ,b= ;
(2)请补全频数分布直方图;
(3)若该校有学生1200人,试估计该校学生每天课外阅读时间超过1小时的人数.