题目内容
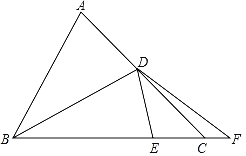
【题目】已知:如图,△ABC中,∠ACB=90°,D在斜边AB上,DE⊥AC,DF⊥BC,垂足分别为E,F.
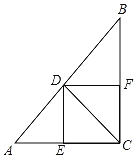
(1)当∠ACD=∠BCD时,求证:四边形DECF是正方形;
(2)当∠BCD=∠A时,求证:![]() .
.
【答案】(1)见解析;(2)见解析
【解析】
(1)由垂直的定义可得出∠DEC=∠DFC,结合∠ECF=90°可得出四边形DECF为矩形,由∠ACD=∠BCD可得出CD平分∠ACB,利用角平分线的性质可得出DE=DF,再利用“邻边相等的矩形是正方形”可证出四边形DECF是正方形;
(2)由∠BCD+∠ACD=∠ACB=90°,∠BCD=∠A可得出∠A+∠ACD=90°,利用三角形内角和定理可求出∠ADC=90°,由∠DCF=∠A,∠DFC=∠ADC=90°可证出△CDF∽△ACD,再利用相似三角形的性质可证出![]() .
.
证明:(1)∵DE⊥AC,DF⊥BC,
∴∠DEC=∠DFC=90°,
又∵∠ECF=90°,
∴四边形DECF为矩形.
∵∠ACD=∠BCD,
∴CD平分∠ACB,
∴DE=DF,
∴四边形DECF是正方形.
(2)∵∠BCD+∠ACD=∠ACB=90°,∠BCD=∠A,
∴∠A+∠ACD=90°,
∴∠ADC=180°﹣90°=90°.
∵∠DCF=∠A,∠DFC=∠ADC=90°,
∴△CDF∽△ACD,
∴![]() .
.

练习册系列答案
相关题目