Question

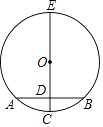
【题目】如图，将长方形纸片ABCD折叠，使边DC落在对角线AC上，折痕为CE，且D点落在对角线D′处．若AB=3，AD=4，则ED的长为

A． B．3 C．1 D．

Answer 1

【答案】A

【解析】

首先利用勾股定理计算出AC的长，再根据折叠可得△DEC≌△D′EC，设ED=x，则D′E=x，AD′=AC﹣CD′=2，AE=4﹣x，再根据勾股定理可得方程22+x2=（4﹣x）2，再解方程即可：

∵AB=3，AD=4，∴DC=3。∴根据勾股定理得AC=5。

根据折叠可得：△DEC≌△D′EC，∴D′C=DC=3，DE=D′E。

设ED=x，则D′E=x，AD′=AC﹣CD′=2，AE=4﹣x，

在Rt△AED′中：（AD′）2+（ED′）2=AE2，即22+x2=（4﹣x）2，

解得：x=。故选A。