题目内容
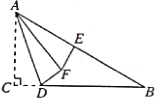
【题目】如图,在正方形![]() 中,
中,![]() 是边
是边![]() 上的动点(与点
上的动点(与点![]() 、
、![]() 不重合),且
不重合),且![]() ,
,![]() 于点
于点![]() ,
,![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() 、
、![]() .
.
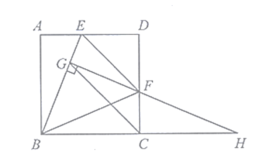
(1)求证:①![]()
![]()
![]() ;②
;②![]() ;
;
(2)若![]() ,在点
,在点![]() 运动过程中,探究:
运动过程中,探究:
①线段![]() 的长度是否改变?若不变,求出这个定值;若改变,请说明理由;
的长度是否改变?若不变,求出这个定值;若改变,请说明理由;
②当![]() 为何值时,
为何值时,![]() 为等腰直角三角形.
为等腰直角三角形.
【答案】(1)①见解析;②见解析;(2)①在点![]() 运动过程中,
运动过程中,![]() 的长度不变,且CG=2;②AE=
的长度不变,且CG=2;②AE=![]() .
.
【解析】
(1)①由题意易得△DEF是等腰直角三角形,即得DE=DF,然后根据正方形的性质和SAS即可证得结论;
②根据全等三角形的性质可得![]() ,根据余角的性质可得
,根据余角的性质可得![]() ,从而可得
,从而可得![]() ,于是可得结论;
,于是可得结论;
(2)①由![]() 、
、![]() 可得
可得![]() ,然后根据直角三角形斜边中线的性质即得结论;
,然后根据直角三角形斜边中线的性质即得结论;
②解法一:如图1,延长![]() 交
交![]() 于点
于点![]() ,易证
,易证![]() 是等腰直角三角形,即
是等腰直角三角形,即![]() ,设
,设![]() ,则
,则![]() ,由
,由![]() 为等腰直角三角形可得
为等腰直角三角形可得![]() ,进而可得
,进而可得![]() ,由
,由![]() 即可求出x的值,即为AE的值;
即可求出x的值,即为AE的值;
解法二:如图2,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,根据AAS易证
,根据AAS易证![]()
![]()
![]() ,所以
,所以![]() ,
,![]() ,从而可得
,从而可得![]() 是等腰直角三角形,由CG=2可得MC的长,进而可得MB的长,即为AE的长;
是等腰直角三角形,由CG=2可得MC的长,进而可得MB的长,即为AE的长;
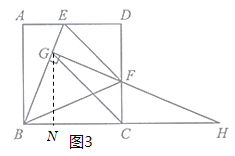
解法三:如图3,过点![]() 作
作![]() 于点
于点![]() ,由B、C、F、G四点共圆可得∠BCG=∠BFG=45°,从而可得
,由B、C、F、G四点共圆可得∠BCG=∠BFG=45°,从而可得![]() 是等腰直角三角形,可得
是等腰直角三角形,可得![]() ,进而可得NH的长,由
,进而可得NH的长,由![]() 即可求出FC,即为AE的长.
即可求出FC,即为AE的长.
(1)证明:①∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴△![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
![]()
![]() ;
;

②∵![]()
![]()
![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;

(2)①在点![]() 运动过程中,
运动过程中,![]() 的长度不变.
的长度不变.
∵![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() (定值);
(定值);
②解法一:如图1,延长![]() 交
交![]() 于点
于点![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() 是等腰直角三角形,即
是等腰直角三角形,即![]() .
.
设![]() ,则
,则![]() .
.
∵![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
在等腰![]() 中,∵
中,∵![]() ,∴
,∴![]() .
.
解得:![]() ,即
,即![]() .
.
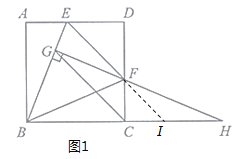
②解法二:如图2,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,则∠MGB=∠CGF,
,则∠MGB=∠CGF,
∵∠M+∠MCG=90°,∠GCF+∠MCG=90°,
∴∠M=∠GCF,
又∵GB=GF,
∴![]()
![]()
![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]()
![]() ,
,
∴![]() ,
,
∴![]() .
.
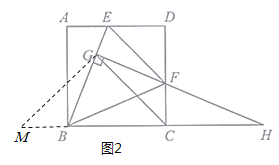
②解法三:如图3,过点![]() 作
作![]() 于点
于点![]() ,
,
∵∠BGF+∠BCF=180°,
∴B、C、F、G四点共圆,
∴∠BCG=∠BFG=45°,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,
∴![]() .
.
∵![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() .
.

 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案【题目】九年级某班准备选拔四名男生参加学校运动会接力比赛,进行了一次50米短跑测验,成绩如下,(单位:秒)6.9 7.0 7.1 7.2 7.0 7.4 7.3 7.5 7.0 7.4 7.3 6.8 7.0 7.1 7.3 6.9 7.1 7.2 7.4 6.9 7.0 7.2 7.0 7.2 7.6
班主任老师按0.2秒的组距分段,统计每个成绩段出现的频数,填入频数分布表,并绘制了频数分布直方图.
成绩段(秒) |
|
|
|
|
|
频数 | 4 | 9 | 7 |
| 1 |
频率 |
| 0.36 | 0.28 | 0.16 | 0.04 |
(1)求a、b值,并将频数分布直方图补充完整;
(2)请计算这次短跑测验的优秀率(7.0秒及7.0秒以下);
(3)成绩前四名的A、B、C、D同学组成九年级某班4×100米接力队,其中成绩最好的A同学安排在最后一棒(第4棒),另外三位同学随机编排在其余三个棒次,画树状图或列表说明B、C两位同学为相邻棒次的概率.