题目内容
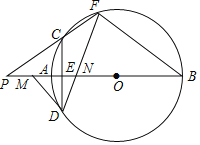
【题目】如图,在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() 在一条直线上,
在一条直线上,![]() ,连接
,连接![]() ,
,![]() 交于点
交于点![]() ,连接
,连接![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 平分
平分![]() .其中正确的是( )
.其中正确的是( )

A.①②③B.①②④C.②③④D.①②③④
【答案】D
【解析】
①根据“SAS”判断△AOC≌△BOD;②根据AOC≌△BOD得到∠COA=∠BOD,再利用两边成比例且夹角相等即可求出![]() ;③由全等三角形的性质得出∠OAC=∠OBD,由三角形的外角性质得:∠AMB+∠OAC=∠AOB+∠OBD,得出∠AMB=∠AOB=40°,④由∠AOB=∠COD,得出当∠DOM=∠AOM时,OM才平分∠BOC,假设∠DOM=∠AOM,由△AOC≌△BOD得出∠COM=∠BOM,由MO平分∠BMC得出∠CMO=∠BMO,推出△COM≌△BOM,得OB=OC,而OA=OB,所以OA=OC,而OA>OC,故④错误;即可得出结论.
;③由全等三角形的性质得出∠OAC=∠OBD,由三角形的外角性质得:∠AMB+∠OAC=∠AOB+∠OBD,得出∠AMB=∠AOB=40°,④由∠AOB=∠COD,得出当∠DOM=∠AOM时,OM才平分∠BOC,假设∠DOM=∠AOM,由△AOC≌△BOD得出∠COM=∠BOM,由MO平分∠BMC得出∠CMO=∠BMO,推出△COM≌△BOM,得OB=OC,而OA=OB,所以OA=OC,而OA>OC,故④错误;即可得出结论.
解:①∵∠AOB=∠COD=30°,
∴∠AOC=∠BOD,
∵OA=OB,OC=OD,
∴△AOC≌△BOD(SAS)故①正确;
②∵△AOC≌△BOD
∴∠COA=∠BOD
∴∠COA-∠A0D=∠BOD-∠A0D,则∠C0D=∠BOA-
∵![]() ,
,![]()
∴![]()
∴![]() ,故②正确;;
,故②正确;;
∵△AOC≌△BOD(SAS),
∴∠OCA=∠ODB,AC=BD, 正确;
∴∠OAC=∠OBD,
由三角形的外角性质得:∠AMB+∠OAC=∠AOB+∠OBD,
∴∠BMA=∠AOB=40°,③正确;
④作OG⊥MC于G,OH⊥MB于H,如图2所示:

则∠OGC=∠OHD=90°,
在△OCG和△ODH中,
 ,
,
∴△OCG≌△ODH(AAS),
∴OG=OH,
∴MO平分∠BMC,④正确;
∵∠AOB=∠COD,
∴当∠DOM=∠AOM时,OM才平分∠BOC,
假设∠DOM=∠AOM
∵△AOC≌△BOD,
∴∠COM=∠BOM,
∵MO平分∠BMC,④正确;
综上所述,正确的有①②③④,答案选D.